De stelling van Pythagoras is de beroemdste stelling. Daarom wellicht werd in september 2017 het wiskundige ‘fake news’ dat de Babyloniërs haar hadden bedacht gretig opgepikt. Toch is er ook écht nieuws: een Japanse hobby-wiskundige bedacht een sublieme veralgemening, al kreeg dit échte nieuws geen weerklank – tot nu.
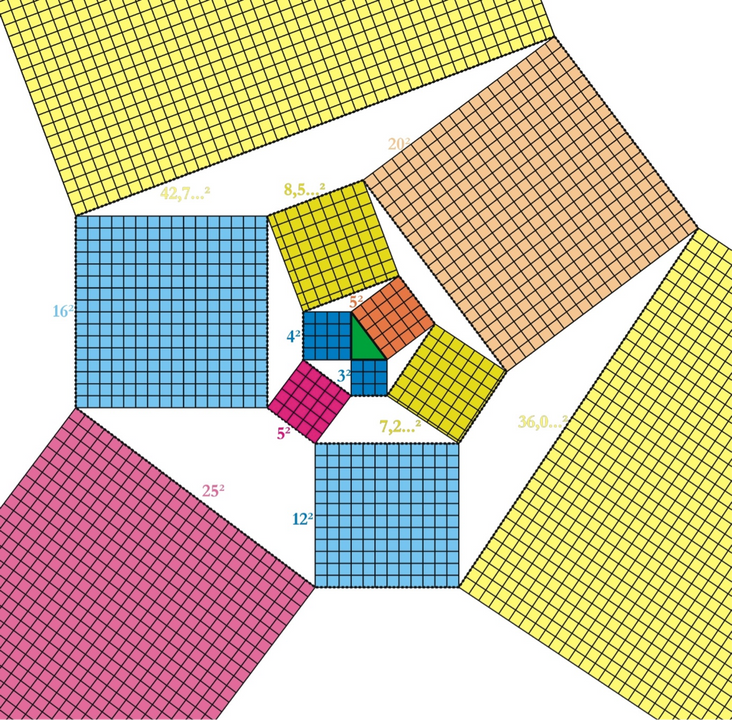
Beschouw de groene rechthoekige driehoek in het midden. Pythagoras stelde dat het oranje vierkant de som is van de blauwe vierkanten. Ebisui zegt nu dat dit ook geldt voor het lichtoranje vierkant en lichtblauwe – en de som van 2 gele is 5 maal 1 paarse, in elk stadium, ‘tot in het oneindige’.
De stelling van Pythagoras stelt dat in een rechthoekige driehoek de som a² + b² van de kwadraten van de lengtes a en b van rechthoekszijden gelijk is aan het kwadraat van de lengte c van de schuine zijde: a² + b² = c². Neem bijvoorbeeld de rechthoekige driehoek met rechthoekszijden 3 en 4 en schuine zijde 5: 3² + 4² = 5² want 9 + 16 = 25. Dit voorbeeld illustreert de stelling met zeer eenvoudige getallen, 3, 4 en 5, en de driehoek daarom wordt de Pythagoreïsche driehoek genoemd, steeds naar de Griekse wiskundige Pythagoras (c. 570–495 BC). Andere eenvoudige voorbeelden zijn de driehoeken met zijden 5, 12 en 13 of deze met zijden 7, 24 en 25.

Hoge bomen vangen veel wind en daarom staat al eens te lezen dat Pythagoras misschien nooit zou geleefd hebben, laat staan dat de stelling dus naar hem vernoemd mag worden. Anderen beweren dat het niet deze bewoner van het eiland Samos was die de stelling als eerste bedacht, maar iemand in het Midden-Oosten, omdat op het 3700 jaar oude ‘Plimpton 322’ kleitablet uit zuid-Irak een reeks getallen staan waaruit mits enige omrekening getallen kunnen worden afgeleid waarvan de som van de kwadraten het kwadraat van een derde getal geeft. Dat is juist, en dit is al bekend sinds een studie uit 1945. Er staat echter geen ‘formule’ op in de aard van a²+b²=c², noch een driehoek, alleen een reeks getallen, en soms kloppen de getallen zelfs niet.
Het tablet werd al gevonden in 1921, en toch leek het in september 2017 alsof dit kleitablet net ontdekt was, nadat de wiskundigen Daniel Mansfield en Norman Wildberger van de Australische Universiteit van Nieuw-Zuid-Wales een zeer verleidelijk persbericht de wereld in hadden gestuurd. Toen leek het alsof pas toen was aangetoond dat er een vroegere versie op stond van de stelling van Pythagoras, terwijl er behalve die studie uit 1945 ook in 1957, 1980, 1993, 1995, 1996 en 2002 publicaties over verschenen waren. Bovendien zou het tablet een bewijs zijn van een superieure beheersing van de wiskunde maar dit was, om enkele moderne termen te gebruiken, een ‘hoax’, ‘fake news’. Niet alleen kenden de Babyloniërs geen ‘driehoeksmeetkunde’, want ze kenden het begrip ‘hoek’ niet, en bovendien staan er ook enkele foute getallen zodat ze zeker niet het ‘werk van een genie’ waren. Wildberger, een zeer bevlogen wiskundige bekend voor zijn dynamische voordrachten, wou zo echter vooral aandacht creëren voor zijn strijdpunt, namelijk zijn gevecht tegen irrationale getallen, die ruimer zijn dan de rationale (dat zijn de breuken met gehele getallen). De Babyloniërs kenden die niet, laat staan een decimale notatie die ze zouden afronden ‘na de decimaal’. Natuurlijk werkten ze dus ‘exacter’, maar ‘betere wiskunde’ was dit niet (zie kaderstukje: ‘De hoax van Pythagoras’).
Mansfield en Wildberger verrasten blijkbaar ook velen door hun bewering dat de bewerkingen op het tablet gebeurden in het zestigtallig stelsel, maar ook dat was zéér oud nieuws. Trouwens, dit stelsel met basis 60 in plaats van 10 komt wellicht uit Afrika. Maar gekruid met wat woestijnstof, omdat een positief bericht over de regio van Irak nu eenmaal welkom is in deze tijden, zag men in alle media Mansfield met witte handschoentjes het kleitablet tonen waarop zogezegd de vroegste versie van de stelling van Pythagoras stond. Die vermaledijde Grieken die het Europese budget in gevaar hadden gebracht, bleken nu ook een stelling gestolen te hebben, terwijl we de wiskunde eigenlijk te danken hebben aan zo onderschatte Arabische regio, zo luidde het. Voor één keer ging een wiskundige stelling erin als zoete koek.
Toch is dit niet zo. Akkoord, het Midden-Oosten, en trouwens ook Indië en China, interesseerden zich aan getallen waarvan de som van de kwadraten van twee van hen het kwadraat van een derde getal geeft, maar dit had niet noodzakelijk betrekking op de zijden van een rechthoekige driehoek. Sommige andere oude ‘teksten’ (of tabletten, of graveringen) bevatten wel bewijzen voor enkele bijzondere gevallen van de stelling en mét een driehoek. Maar het was wel degelijk de Griek Pythagoras die als eerste de stelling aantoonde, als stelling, en niet door een aantal numerieke voorbeelden. En dat is een hemelsbreed verschil. Het is gewoon het verschil tussen een beetje spelen met getallen en wiskunde. Rik Verhulst onderbouwde het belang hiervan in zijn boek ‘De zes hamerslagen van de westerse rationaliteit’ (2006).
De stelling
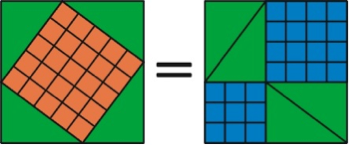
Pythagoras ging als volgt te werk. In twee vierkanten staan vier identieke driehoeken, die evenwel verschillend geschikt zijn. De overblijvende ruimtes, waarvan de één een vierkant is met oppervlakte c² en de ander een som van twee vierkanten met oppervlaktes a² en b², moeten dus gelijk zijn, en daarom is c² gelijk aan a² plus b². Eenvoudig, duidelijk, en het is een redenering, geen oplijsting van numerieke voorbeelden.
De stelling van Pythagoras kreeg zijn grote roem omdat ze in ‘De Elementen’ stond, een serie van dertien boeken geschreven door de Griek Euclides (±300 v. Chr.), waarin hij een kleine vijfhonderd toen bekende stellingen en bewijzen logisch rangschikte. Deze wiskunde uit de vijfde eeuw voor Christus werd door Euclides’ systematische benaderingswijze de grootste stimulans in de ontwikkeling van de wiskunde. Lange tijd wedijverden ‘De Elementen’ met de Bijbel om de titel van bestseller van het jaar. Euclides bewees de stelling van Pythagoras wel op een andere manier, door te stellen dat elk van de kleinere vierkanten gelijk is aan een rechthoekig deel van het grotere vierkant en de som van die twee rechthoekige delen precies het grote vierkant is. Zijn redenering werd gevisualiseerd in ontelbare tekeningen gedurende 2000 jaar.
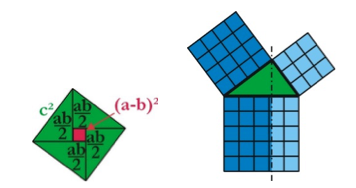
Niet in het minst omwille van de faam van ‘De Elementen’ probeerden velen de stelling van Pythagoras op nog andere manieren te bewijzen. E. S. Loomis verzamelde zowaar driehonderdzeventig bewijzen (370!) in zijn boek ‘The Pythagorean Proposition’ (uitgaven in 1928, 1940, 1968 en 1972). Zelf verkies ik een bewijsje dat net zoals dit van Pythagoras met vier groene driehoekjes werkt en een eenvoudig algebraïsche uitwerking heeft: c² = 4.ab/2 + (a-b)² = 2ab + a² + b² - 2ab = a² + b² (zie figuur). Technopolis en andere wetenschapsparken tonen al eens een opstelling waarbij men water uit de twee kleine vierkanten kan laten stromen in het grote vierkant om zo hun gelijkheid te illustreren. c2 = a2 + b2 . {\displaystyle c^{2}=a^{2}+b^{2}.}
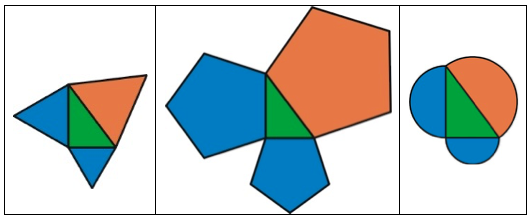
Niet alleen kwamen er meer bewijzen, er kwamen ook talrijke veralgemeningen. Als er op de zijden van de driehoek andere gelijkvormige figuren worden geplaatst dan vierkanten, dan ‘lukt de stelling ook’, zo bleek. Gelijkvormige driehoeken, regelmatige vijfhoeken, of gelijkvormige stukken cirkel, het doet er allemaal niet toe: de som van de oppervlakten van de figuren op de rechthoekszijden is gelijk aan de oppervlakte van de figuur op de schuine zijde. De reden is natuurlijk dat de oppervlakte van een dergelijke figuur evenredig is met het kwadraat van een zijde (d.w.z. gelijk is aan het kwadraat van een zijde maal een vast getal).
Ook hier is het merkwaardig hoeveel culturen doorheen de tijden mogelijke veralgemeningen hebben bestudeerd. Er kwamen trouwens ook versies voor willekeurige driehoeken, met parallellogrammen in plaats van vierkanten, en 3D versies met ruimtelijke interpretaties. En natuurlijk kwamen er in de tijden van de moderne wiskunde ook zeer abstracte versies waarin elke verwijzing naar een driehoek en naar kwadraten of vierkanten verdwenen schijnt. Maar uiteindelijk, na 2000 jaar zoeken en bestuderen over de hele wereld, bleek alles gezegd, berekend en beredeneerd.
De stelling van Pythagoras-Ebisui
Inderdaad, vandaag zijn de Euclidische geometrische vraagstukken passé. Geen punten, lijnen, vlakken, cirkels en bollen met hun onderlinge relaties in het vlak en in de ruimte meer in het onderwijs noch in de ‘hardcore wiskunde’, op enkele uitzonderingen na. De benaming ‘elementaire geometrie’ voor dit studiegebied verwees oorspronkelijk naar de titel van Euclides’ werk, maar vandaag krijgt het adjectief ‘elementair’ soms de connotatie van ‘simpel’. Het enige dat nog overblijft, is de stelling van Pythagoras (en misschien deze van Thales) al bevat geen enkel hedendaags tekstboek een bewijs met driehoekjes die in een vierkant passen zoals bij Pythagoras of Euclides – tenzij als ‘leuke bladvulling’.
Toch vinden niet alle wiskundigen dat dit zo hoeft te zijn en dat de stelling van Pythagoras best aan een revival toe mag zijn. Eén van hen is de Oostenrijker Gunter Weiss (°1946), een professor van de Universiteit van Wenen die vanaf 1995 aan het Duitse TU Dresden werkte en jarenlang de drijvende kracht was van de ‘International Society for Geometry and Graphics’ (ISGG). In sommige van zijn publicaties en voordrachten stelt hij vraagstukken voor in Euclidische aard, die wél de nieuwsgierige hedendaagse lezer en toehoorder prikkelen. Hij meent dat ook vandaag nog de onderwerpen van Euclides uitdagende voorbeelden kunnen bieden zodat leerlingen en studenten competentie kunnen verwerven in het logisch redeneren. Bovendien bestaat er nu software zoals Geogebra die toelaat om aan Euclides’ figuren beweging toe te kennen door de punten, rechten en cirkels te laten variëren, zodat deze wiskunde ‘tot leven komt’.2 ‖ v ‖ 2 + 2 ‖ w ‖ 2 = ‖ v + w ‖ 2 + ‖ v − w ‖ 2 , {\displaystyle 2\|\mathbf {v} \|^{2}+2\|\mathbf {w} \|^{2}=\|\mathbf {v+w} \|^{2}+\|\mathbf {v-w} \|^{2}\ ,} d s 2 = d r 2 + r 2 d θ 2 . {\displaystyle ds^{2}=dr^{2}+r^{2}d\theta ^{2}\ .}
Wat in het bijzonder de stelling van Pythagoras betreft, illustreert Weiss dit met een resultaat van een Japanse hobby-wiskundige, Hirotaka Ebisui (zie kaderstukje). Ebisui verbond de hoekpunten van de vierkanten die volgens de klassieke stelling van Pythagoras op de zijden van een rechthoelkige driehoek staan opnieuw met vierkanten. Hij stelde nu vast dat de som van de oppervlakte van twee ervan gelijk is aan vijf maal de oppervlakte van het derde vierkant. Vervolgens verbond hij de hoekpunten van deze nieuwe vierkanten nogmaals met vierkanten. Nu stelde hij vast dat, net zoals bij de aanvankelijke stelling van Pythagoras, de som van de oppervlakte van twee vierkanten gelijk is aan de oppervlakte van het derde vierkant. En dit proces kan steeds verder gezet worden: in een volgende fase is de som van de oppervlakte van twee ervan weer gelijk aan vijf maal de oppervlakte van het derde vierkant, en daarna is de som van de oppervlakte van twee vierkanten gelijk is aan de oppervlakte van het derde vierkant, enzovoort.
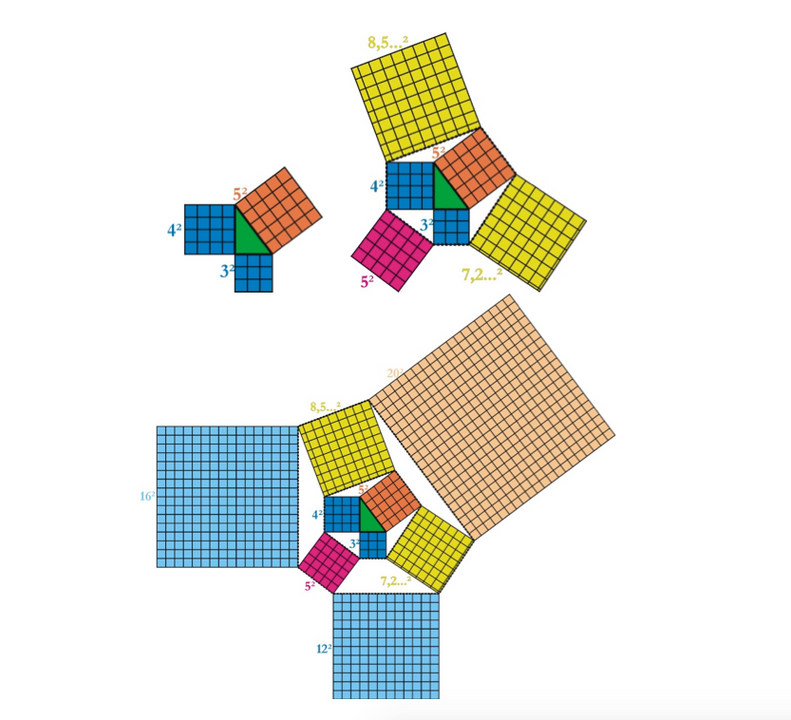
De opbouw van de stelling van Pythagoras-Ebisui, waarvan de openingsillustratie de vierde fase is: oranje = blauw + blauw; paars maal vijf = geel + geel.
Het is een wonderlijke veralgemening, vindt Weiss. Vanwaar die ‘vijf’? En waarom komt de stelling zelf terug na elke tweede ‘laag’? Weiss was er op gestoten na een toevallige ontmoeting met de Japanse amateurwiskundige, maar hij bewees ze wiskundig ‘zoals het hoort’, en probeert ook om ze zoveel mogelijk kenbaar te maken. En hij heeft gelijk: 2000 jaar na Pythagoras zijn de wonderen de wereld nog niet uit. Ook niet het wonder van Pythagoras.



