Pi-dag - the long version

Dat er op $\pi$-dag elk jaar opnieuw iets te vieren valt, dat is duidelijk. Maar vandaag 14 maart 2019 meer dan anders: vandaag start het Platform Wiskunde Vlaanderen, dat de bedoeling heeft de wiskundige gemeenschap in Vlaanderen te verenigen en meer uitstraling te geven. Meer erover lees je op de website: wwww.platformwiskunde.be. Als je daar naartoe surft, dan kom je met wat geluk uiteindelijk weer hier terecht, waar we je ter vermaak een hele resem weetjes over het getal $\pi$ en $\pi$-dag voorschotelen.

Wist je al dat:

• $\ldots$ het vandaag $\pi$-dag is? Waarom? Omdat de datum 14 maart in de Amerikaanse schrijfwijze genoteerd wordt als 3/14 en 3,14 is een benadering voor het getal $\pi$.

• $\ldots$ het getal $\pi$ tot op 500 cijfers na de komma gelijk is aan:
  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194913

• $\ldots$ het getal $\pi$ de verhouding geeft van de omtrek van een cirkel tot de diameter? Of van de oppervlakte van een cirkel tot het kwadraat van de straal?

• $\ldots$ je het getal $\pi$ ook kan vieren op 22 juli, omdat 22/7 een benadering geeft voor $\pi$? We noemen deze dag dan ook: pi approximation day.

• $\ldots$ de uitvinder van pi-dag een fysicus is? Larry Shaw begon er mee in 1988; of, als je dit niet gelooft
   
• $\ldots$ pi-dag in feite geen echte feestdag is maar uitgevonden is door wiskundebedrijven met de bedoeling om meer wiskunde te kunnen verkopen?
   
• $\ldots$ waarschijnlijk de eerste keer dat de notatie $\pi$ gebruikt wordt, is in het boek Synopsis Palmariorum Mathesos (1706) (vrij vertaald: een nieuwe inleiding tot de wiskunde) van ene William Jones (1675-1749).

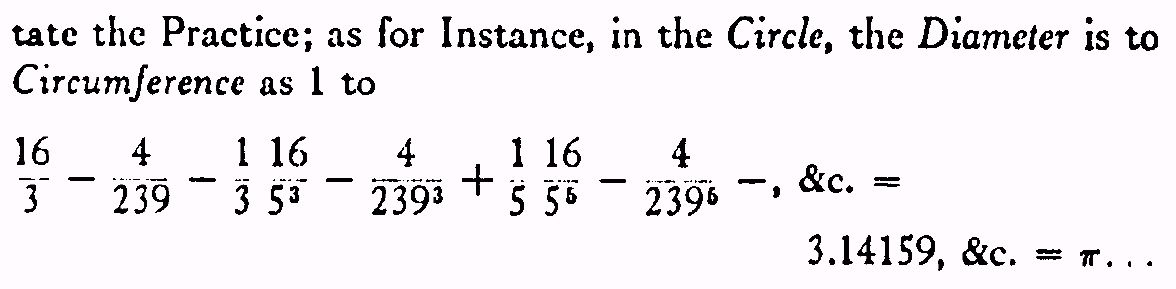
De grote wiskundige Leonhard Euler (1707-1783) zorgde voor de verspreiding van deze notatie.

• $\ldots$ er absoluut geen regelmaat of periode zit in de decimalen van het getal $\pi$? Er is dan ook geen breuk met gehele teller en noemer te vinden die als waarde $\pi$ heeft. Dat heeft voor gevolg dat je met het getal $\pi$ in het Guinness Book of Records kan komen (zoals de mensen op de volgende foto die recordhouder zijn in de categorie Met het grootste aantal mensen het symbool voor het getal $\pi$ vormen -- 14 maart 2018).

• $\ldots$ het record meeste decimalen van $\pi$ berekenen stond tot 13 maart op naam staat van Peter Trüb, die in 2016 $\pi^e$ biljoen decimalen van $\pi$ heeft berekend? Dus 22,459,157,718,361 cijfers. Sinds vandaag, 14 maart, staat het op naam van de Japanse Google Cloud-ontwikkelaar Emma Haruka Iwao, die 31,415,926,535,897 decimalen (makkelijker te onthouden dan het vorige record) berekende in the cloud. De berekening duurde 121 dagen. Meer lees je hier.
• $\ldots$ Archimedes al rond het jaar 250 v. Christus benaderingen berekende voor het getal $\pi$? Hij deed dit door te vertrekken van een cirkel met straal 1 en de halve omtrek te berekenen van ingeschreven en omgeschreven regelmatige veelhoeken met een toenemend aantal zijden.

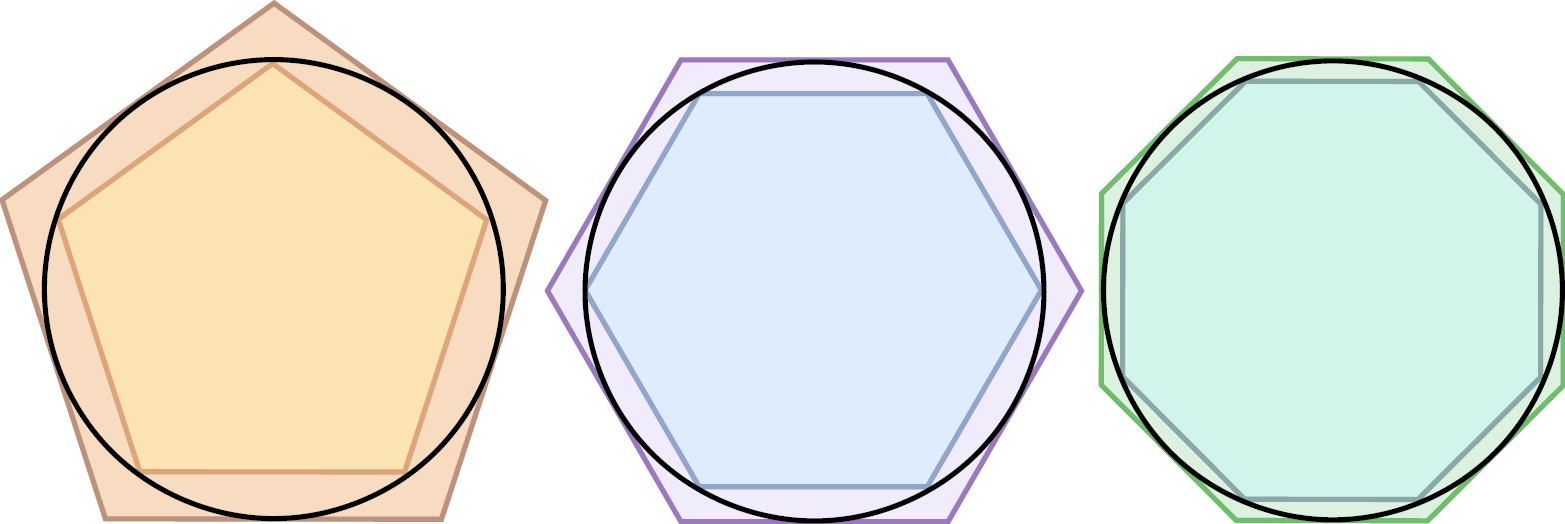
Deze waarden geven begrenzingen naar onder en naar boven voor het getal $\pi$. Het getal $\pi$ wordt daarom soms ook de constante van Archimedes genoemd.

• $\ldots$ de meest gebruikte formule voor de berekening van decimalen van $\pi$ de formule van Machin (1706) is? Hier is ze: $$\frac{\pi}{4} = 4 \cdot {\rm Bgtg} \frac{1}{5} -  {\rm Bgtg} \frac{1}{239} $$ Deze formule kan heel eenvoudig bewezen worden m.b.v. complexe getallen (volgt uit $(5+i)^4=2(1+i) (239+i)$).
   
• $\ldots$ als men je op $\pi$-dag vraagt hoeveel decimalen van $\pi$ je kent, het beste antwoord is: allemaal, maar ik ben nu nog aan de volgorde aan het werken?
   
• $\ldots$ de oudste exacte uitdrukkingen waarmee je het getal $\pi$ kan berekenen, de volgende zijn?
  (1579) de productformule van Vieta $$ \frac{2}{\pi} \!= \textstyle\!\sqrt{\frac{1}{2}} \!\cdot\! \sqrt{\frac{1}{2} \!+\! \frac{1}{2} \!\cdot\! \sqrt{\frac{1}{2}}} \!\cdot\! \sqrt{\frac{1}{2} \!+\! \frac{1}{2} \!\cdot\! \sqrt{\frac{1}{2} \!+\! \frac{1}{2} \!\cdot\! \sqrt{\frac{1}{2}}}} \!\cdot\! \ldots $$
  (rond 1650) de productformule van Wallis $$ \frac{2}{\pi} = \frac{1\cdot 3}{2 \cdot 2} \cdot \frac{3 \cdot 5}{4 \cdot 4} \cdot \frac{5 \cdot 7}{6 \cdot 6} \cdot \ldots $$
  (1655) de kettingbreuk van Lord Brouncker $$ \frac{4}{\pi} = 1 + \cfrac[l]{1^2}{2+\cfrac[l]{3^2}{2+\cfrac[l]{5^2}{2 + \cfrac[l]{7^2}{2 + \cfrac[l]{9^2}{\ldots}}}}} $$
  (rond 1670) de reeks van Gregory-Leibniz $$\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \ldots $$ (deze was eigenlijk al gekend rond 1400 door de Indische wiskundige Madhava van Sangamagrama).
   
• $\ldots$ Ludolph Van Ceulen (1540-1610), een Duits wiskundige, een groot deel van zijn leven spendeerde aan het (met de hand) uitrekenen van decimalen van $\pi$? Hij deed dit met de methode van Archimedes en geraakte tot aan de 35-ste decimaal. Daarom wordt $\pi$ ook het Ludolfiaans getal genoemd.

• $\ldots$ dit hem werd nagedaan door William Shanks (1812-1882), een Brits amateur-wiskundige? Hij rekende 20 jaar aan de eerste 707 decimalen. Hij had een vaste routine: 's morgens decimalen berekenen, 's namiddags de berekeningen checken.
   
• $\ldots$ William Shanks een fout had gemaakt bij het 527ste cijfer na de komma, en dat de rest van zijn berekeningen dus ook waardeloos was?
  
  Seven hundred seven, Shanks did state,
  Digits of $\pi$ he would calculate
  And none could deny
  It was a good try
  But he erred in five twenty-eight. 
  
  (auteur: N. Rose)
   
• $\ldots$ de 707 decimalen berekend door Shanks in 1937 op het plafond van een van de zalen van het Palais de la Découverte in Parijs werden geschilderd, en dat de foute decimalen pas in 1947 werden verbeterd?

• $\ldots$ de Japanse ingenieur Akira Haraguchi de eerste 111700 decimalen van $\pi$ uit het hoofd kent? In oktober 2006 heeft hij er 100000 opgezegd. Naar eigen zeggen doet Akira niets speciaals op $\pi$-dag, behalve misschien iets langer aperitieven dan anders.
   
• $\ldots$ het getal $$\frac{\ln (640\,320^3+744)}{\sqrt{163}}$$ tot op 30 cijfers na de komma gelijk is aan het getal $\pi$?
   
• $\ldots$ er in 1998 een langspeelfilm is uitgekomen met als titel $\pi$?
   
• $\ldots$ in de Amerikaanse staat Indiana de waarde van het getal $\pi$ in 1897 bijna bij wet is vastgelegd op 3,2?
   
• $\ldots$ er heel wat mnemotechnische middelen zijn om te decimalen van $\pi$ te helpen onthouden? Bijvoorbeeld:
  How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.
   
• $\ldots$ er een dichtvorm gebaseerd is op het getal $\pi$? Hier is een voorbeeld ervan (let op het aantal lijnen per strofe) door Drs. P:
  
  Pi-sonnet
  
  Drie, een, vier, een en vijf ... verstijft u even?
  Goed - tweeëntwintig dan, gedeeld door zeven
  Precies, dat is wat ik bedoelde: $\pi$
  
  Een Fransman wou daar een sonnet mee maken
  
  Die reeks vertoont wel weinig symmetrie
  Maar veertien in totaal is een gegeven
  Twee losse regels tot refrein verheven -
  Zo wordt het een gedicht, wel wis en drie 
  
  Jacques Bens wist dus een nieuw sonnet te maken
  
  Wie zou hiervan niet in vervoering raken?
  Na twintig jaar belandde 't goed en wel
  In onze taal. U moet van ijver blaken
  Om op zo'n innovatie in te haken
  (Hij noemde die sonnet irrationnel)
   
• $\ldots$ dat er wetenschappers zijn die vinden dat $\pi$ verkeerd is? Ze bedoelen hiermee dat het een foute keuze was het getal $3,\!1415...$ voor te stellen met de afkorting $\pi$. Het was logischer geweest het dubbele, namelijk $6,\!2831$ met de letter $\pi$ aan te duiden. Het zou het lezen van de $\pi$-klok alvast een stuk gemakkelijker maken: links zie je de huidige situatie, rechts die bij de andere keuze.

• $\ldots$ er niet zoveel oneindige reeksen bekend zijn waar in de som $\pi^5$ voorkomt? Dit zijn er alvast twee: $$1+\frac{1}{2^{15}}\sum_{n=1}^\infty P(n) \frac{(n-1)!^{10}}{\left(\frac{1}{2}\right)_{\!n}^5 \left(\frac{1}{2}\right)_{\!n+1}^5} = \frac{\pi^5}{2^5}$$ en $$ 1-\frac{1}{2^5}\sum_{n=1}^\infty P(n) \frac{\left(\frac{1}{2}\right)_{\!n-1}^5 \left(\frac{1}{2}\right)_{\!n}^5}{n!^{10}} = \frac{2^5}{\pi^5}$$ met $P(n)$ in beide reeksen gelijk aan $1280n^8-640n^6+160n^4-20n^2+1$. We gebruiken hierbij de Pochhammer notatie: $(a)_n=a\cdot (a+1)\cdots (a+n-1)$.

• $\ldots$ we ondertussen ook weten waarom precies pi(e) gebruikt wordt als benaming voor deze constante?

• $\ldots$ we ondertussen ook begrijpen waar de pi in 'piano' vandaan komt?

• $\ldots$ er veel pandigitale benaderingen zijn voor $\pi$?
  Pandigitaal betekent dat elk cijfer van 1 tot 9 er precies 1 keer in voorkomt. Hier is een voorbeeld. Het getal $$3 + \frac{1-(9-8^{-5})^{-6}}{7+2^{-4}} $$ geeft een benadering voor $\pi$ die tot op 9 cijfers na de komma correct is.
  (Merk op dat er een veel betere pandigitale benadering bestaat voor het getal e: $$\left(1+9^{-4^{7\cdot 6}}\right)^{3^{2^{85}}} $$ is tot op 18457734525360901453873570 decimalen correct.)
   
• $\ldots$ in de 21ste aflevering (``Marge in de boeien") van het vierde seizoen van de reeks The Simpsons de eigenaar van de Springfieldse Kwik-E-Mart Apu Nahasapeemapetilon in de rechtbank zegt dat hij in staat is 40000 decimalen van het getal $\pi$ op te zeggen? Apu merkt verder terecht op dat het 40000ste cijfer gelijk is aan 1. Blijkbaar hebben de schrijvers van deze aflevering deze scene voorbereid door aan de NASA te vragen wat de 40000ste decimaal van $\pi$ is. NASA heeft hen dan een uitprint gestuurd van de eerste 40000 cijfers.

• $\ldots$ de kwadratuur van de cirkel wel optisch mogelijk is? Geen trucage, wel een spiegel.

En dan hebben we het nog niet gehad over het naaldenexperiment van Buffon (een langdradige manier om met behulp van een naald en een blad papier met lijnen benaderingen te vinden van $\pi$), de Indische wiskundige Ramanujan (die iets had met $\pi)$, het 154 bladzijden tellende gedicht Poème Pi van de Franse groep Oulipo, het feit dat je met het getal $\pi$ kan bewijzen dat er oneindig veel priemgetallen zijn, en nog veel meer. Dat $\pi$ niet zomaar een verzinsel is van wiskundigen maar ook echt in de natuur voorkomt, dat kan je zien op deze foto van een s$\pi$innenorchis: