“Elke dag een ziekenhuis erbij”? Nee!

Op 23 oktober blokletterde een kwaliteitskrant het als een grote titel: “Elke dag een ziekenhuis erbij”. Op het eerste gezicht lijkt het alsof ze hiermee de viroloog Steven Van Gucht had geciteerd, die de dag ervoor over het aantal ziekenhuisopnames het volgende had verklaard: “Om de tien dagen zien we op dat vlak een verdubbeling”. Het is niet zozeer het aantal dagen, maar de manier waarop de groei wordt beschreven die een probleem stelt: indien een constante hoeveelheid telkens wordt toegevoegd, dan is dit niet hetzelfde als indien een hoeveelheid steeds wordt verdubbeld. Om de zoveel dagen ‘een ziekenhuis erbij’ is véél minder dramatisch dan ‘een verdubbeling van het aantal opnames’.

In een Eos blog maakte filosofe Sylvia Wenmackers de vergelijking met samengestelde interest: ‘Hoe klein het basispercentage ook is, als het op gezette tijden ergens wordt bijgeteld, dan stijgt het totaal exponentieel’. Ook zij spreekt nu van ‘erbij’ tellen, maar het hangt er hier wel van af waar men dit basispercentage op toepast. Bij een percentage op steeds hetzelfde basisbedrag spreekt men van enkelvoudige interest; bij een percentage op het basisbedrag plus de geaccumuleerde interest, krijg je inderdaad samengestelde interest. Stel, zoals in die blog, dat je 100 euro hebt en je 1% interest per jaar krijgt. Enkelvoudig worden de interest en het totale bedrag over verschillende jaren: 1 en 100+1=101; 1+1=2 en 100+2=102; 2+1=3 en 100+3=103; enzovoort, maar samengesteld is dit 1 en 100+1=101; 101×0,01=1,01 en 101+1=102,01; 102,01×0,01=1,0201 en 102,01+1,0201= 103,0301; enzovoort… In het eerste geval is dit ‘ergens’ waarvan men het basispercentage van neemt steeds 100, maar in het tweede is dit 100; 101; 102,01; enzovoort. En dat is een heel verschil, zoals Sylvia Wenmackers uitlegde.

Ik poogde zelf die exponentiële groei uit te leggen aan de hand van een beschrijving die ook Al Gore reeds gebruikte in zijn documentaire over de klimaatsverandering, ‘An unconvenient truth’: ze volgt een ‘hockey stick curve’. Het handvat van een ijshockeystick die platligt volgt ongeveer de horizontale as, maar het deel waarmee de puck wordt weggeslagen gaat snel verticaal omhoog. Omdat een ijshockeypuck meestal krachtig wordt geslagen, geeft dit een mooi bijna filmisch beeld voor zo’n exponentiële kromme: ze ‘schiet’ als het ware zeer snel omhoog na een aanvankelijk bijna horizontaal deel.

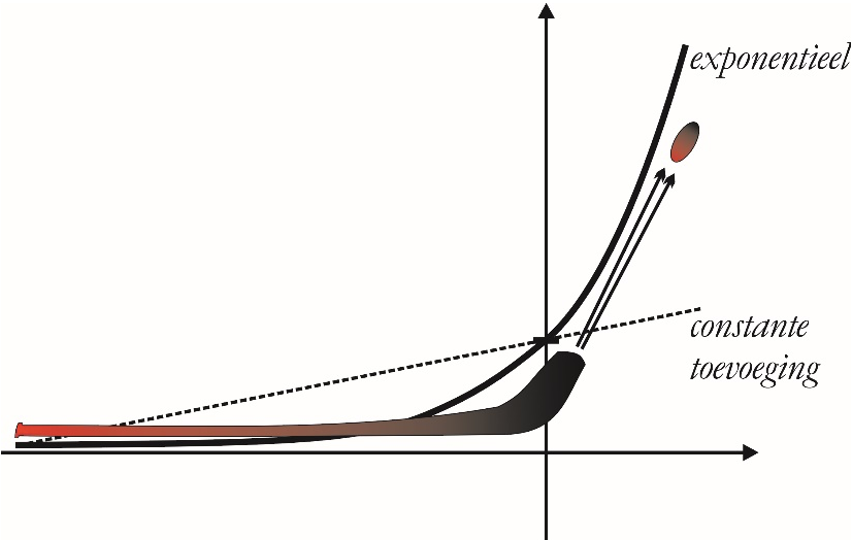
En inderdaad, een virus vermenigvuldigt zich dus volgens een exponentieel proces, zoals ik in het hierboven vermelde artikel probeerde te illustreren aan de hand van rijstkorrels op een schaakbord. Als hun aantal zich steeds verdubbelt, zal 1 korrel op het eerste vak vervolgens 2 geven, dan 2²=4, dan 2³=8, dan 16, dan 32, enzovoort, tot wanneer er een onuitspreekbaar groot getal wordt bereikt op het 64^ste vakje.

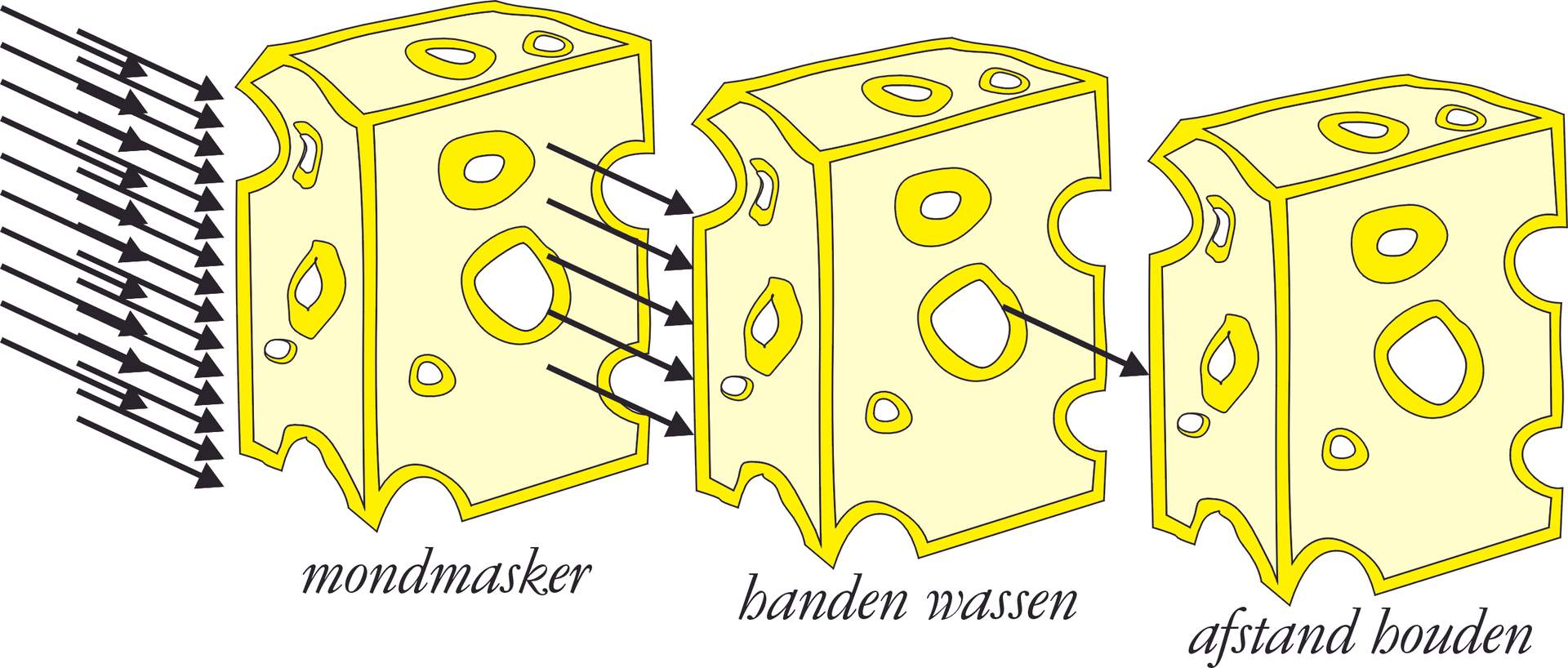
Anderzijds schuilt hierin ook het goede nieuws: veronderstel dat een mondmasker slechts 4/5 van de virussen tegen houdt. Dan komt er een 1/5-deel dus wel doorheen, zoals sommige fervente critici beweren. Veronderstel nu dat ook het handwassen slechts 4/5 van de coronaatjes tegenhoudt. Dan komt er weer 1/5 door. Deze cijfers zijn steeds louter hypothetisch, en aan de hoge kant ingeschat, om de criticasters tegemoet te komen. En neem het afstand houden, laat ons ook daar stellen dat dit slechts voor 4/5 efficiënt is. Het totale effect is dan dat (1/5)³ van de virussen door alle barrières heen komt, of 0,008 = 0,8%. Dat is dus bijna niets, ondanks de hoge ingeschatte waarden, want de verschillende barrières volgen ook een exponentieel proces. Door het combineren van verschillende maatregelen kunnen we dus die verdoemde exponentiële viruskromme als het ware tegen zichzelf gebruiken.