Los van pandemische motieven kan het sluiten van de landsgrenzen en het kiezen voor een totaal isolement soms heilzaam zijn voor een volk.
Neem nu Japan bijvoorbeeld. Het leefde tijdens de zogenaamde Edo-periode van 1603 tot 1867 vrijwillig geïsoleerd van het westen, en kende hierdoor boeiende economische, filosofische en culturele ontwikkelingen. Een groot deel van de Japanse eigenheid zoals we die nu kennen, is toen ontstaan of tot bloei gekomen. Hierbij denken we aan geisha’s of haiku’s, maar ook (en vooral) aan sangaku’s.

Deze gekleurde houten tabletten werden in de Edo-periode opgehangen in Shinto-heiligdommen of Boeddhistische tempels, waarschijnlijk als geschenk voor goden of heiligen.
Met weinig of geen tekst illustreren sangaku’s een zelfbedachte meetkundige eigenschap over driehoeken, vierkanten, ellipsen en vooral cirkels. Zeg nu zelf, veel ontroerender en edeler kan een geschenk niet zijn. Omdat een sangaku bovendien zichtbaar was voor de andere tempelbezoekers, streefde de maker meestal naar een esthetische geometrie en imponerende complexiteit. Een YouTube-battle avant la lettre dus. De ideale sangaku is een mystiek verbond tussen zijn artistieke schepper, een zuivere meetkundige eigenschap (god) en de uitgedaagde toeschouwer.
Vele sangaku’s zijn ons bekend dankzij het missionariswerk van de Japanse wiskundige Hidetoshi Fukagawa in Amerika. Lees bijvoorbeeld
H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, 1989.
of H. Fukagawa, A. Rothman, Sacred Mathematics: Japanese Temple Geometry, 2008.
Hieruit tonen we deze vijf-cirkels-sangaku:
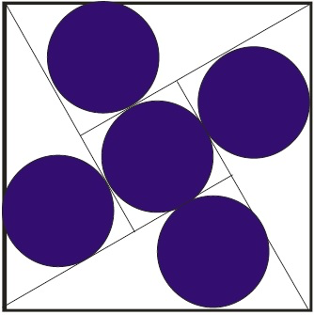
Als u zich afvraagt hoe men er in geslaagd is om vijf identieke cirkelschijven op deze manier in een vierkant te klemmen, dan kunnen we u geruststellen. Die vraag is namelijk exact de bedoeling van deze sangaku. Een goede student met meetkundige bagage kan uitrekenen dat bovenstaande configuratie enkel lukt indien de straal R van de cirkels zich verhoudt t.o.v. de zijde Z van het vierkant als:
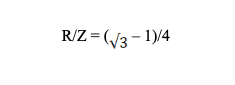
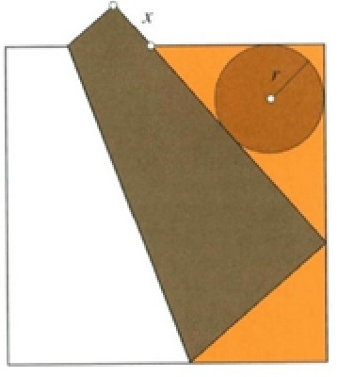
Al moet gezegd dat afhankelijk van het culturele kader of de context van het vraagstuk, het niet altijd de numerieke oplossing is die gezocht wordt. Zo werden in de Griekse oudheid meetkundige problemen gekraakt met zuivere passer-en-liniaal constructies, terwijl in het Edo-tijdperk de meetkunde wel eens met behulp van origami bedreven werd. Probeer dit laatste eens zelf met de volgende (bescheiden) uitdaging. Leg een rond bierviltje (bijvoorbeeld) in de hoek van een vierkant tafelkleedje of kaartmatje. Als we het vierkant plooien zoals hieronder aangegeven, totdat een zijde de cirkel raakt, dan heb je de straal van de cirkel “bepaald” als de uitstekende lengte x.
Net zoals vele andere sangaku’s is de vijf-cirkels-sangaku een voorbeeld van een wiskundige stapeling. De objecten die gestapeld worden mogen van willekeurig vorm, omvang of dimensie zijn, zolang ze elkaar maar niet overlappen. Een mooie illustratie is de stapeling van 19 identieke cirkels in een gelijkzijdige driehoek zoals bedacht door de Hongaarse wiskundige Farkas Bolyai.
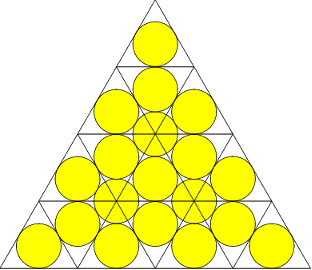
Deze was bedoeld als optimaal plantschema voor bomen. Al zien wij eerder toepassingen in onze wijnkelder. Hongaren blijken toevallig erg bekwaam in deze discipline. Zo zoekt en vindt Zsófia Ruttkay ook inspiratie in de natuur voor “dichtbegroeide” cirkelstapelingen, meer bepaald bij de uitzetting van waterlelies (in de tuin van Monet, of als we in het thema willen blijven, in de vijver van een boeddhistische tempel):

In de loop van de 20ste eeuw is het stapelen een aparte wiskundige discipline geworden. Wereldwijd zijn er mensen die professioneel hun echte dagen en denkbeeldige containers vullen met cirkels of bollen of met wat dan ook hun pad kruist. Meestal is de uitdaging van deze rekkenvullers van de wiskunde het maximaliseren van de stapeldichtheid, of anders gezegd, het minimaliseren van de verspilde (lege) ruimte. De vakkennis van een meetkundige expert in het stapelen van cirkels kan soms goed van pas komen. Hij weet hoeveel flessen wijn in een doos geraken, en hij heeft het inzicht hoe zoveel mogelijk ronde bierkaartjes uit een rechthoekig vel te snijden. Bovendien, in het geval hij graag moeilijke woorden gebruikt, weet hij waar hij de constellatiepunten moet plaatsen voor een optimale kwadratuuramplitudemodulatie.
Maar een wiskundige cirkelinpakker weet ook hoeveel stoelen je in een aula of theaterzaal kan opstellen (en hoe), met de garantie op een minimale afstand tussen de toeschouwers. Hieronder wordt dit duidelijk gemaakt. Wie de kunst beheerst om 5 cirkels optimaal te stapelen in een (blauw) vierkant, weet ook waar vijf mensen te plaatsen in een (rood) vierkant zodat de afstand tot de dichtste buur zo groot mogelijk is. En dat is exact zoals hieronder getoond wordt:
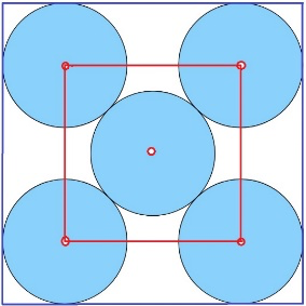
(Hierbij verontschuldigen we ons voor de veelvoorkomende academische misvatting om mensen te verwarren met oneindig kleine punten.)
Hieronder zie je hoe onze professionele cirkelstapelaar uit een (blauw) papieren vierkant N cirkels knipt om zo weinig mogelijk aan tussenliggende ruimte te verkwisten. Of hoe hij N puntmensen plaatst in een (rode) vierkante kamer om de kleinste afstand tussen twee personen te maximaliseren.


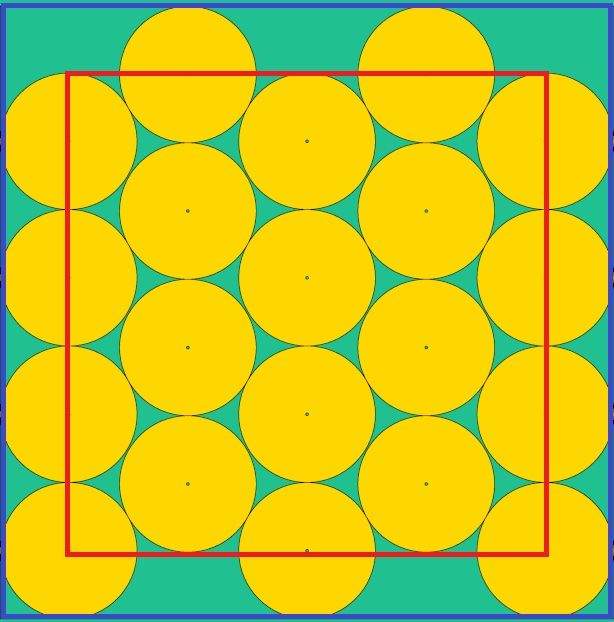
Deze voorbeelden suggereren dat optimale cirkelpatronen zich niet door een vaste formule laten bepalen. Eigenlijk is het patroon met de twintig cirkels nog het minst verrassend, want dit is de oplossing die iedere wijnverzamelaar of transporteur van soepblikken al bedacht heeft. Het is de bekende hexagonale schikking, waarbij iedere cirkel exact zes andere zou raken indien de container zich in alle richtingen oneindig uitstrekte. Volgens het Theorema van Thue (1890) geeft dit hexagonaal patroon de optimale stapeling van identieke cirkels in een onbegrensd vlak, waarbij een maximale dichtheid van ongeveer 91% (π/om exact te zijn) behaald wordt.

Het maakt ons in ieder geval nederig om te merken dat bijen geen wiskunde nodig hebben om hun honingdruppels in dit optimale patroon van regelmatige zeshoeken te laten opdrogen.
Ieder verschillend aantal cirkels lijkt wel om een ad-hocoplossing te vragen, maar er komt echt wel wat wiskundig vakmanschap bij kijken. En natuurlijk ook computerrekentijd. Anderzijds is het zo dat origamiwiskundigen (ja, die zijn er ook) zoals Erik Demaine en Robert Lang hebben aangetoond dat er nooit een efficiënt algoritme zal gevonden worden om een optimale stapel van cirkels te berekenen voor een rechthoekig stuk papier, wat zij betreuren want dit was handig geweest bij het tekenen van bepaalde vouwpatronen.
Ieder verschillend aantal cirkels lijkt wel om een ad-hocoplossing te vragen, maar er komt echt wel wat wiskundig vakmanschap bij kijken. En natuurlijk ook computerrekentijd. Anderzijds is het zo dat origamiwiskundigen (ja, die zijn er ook) zoals Erik Demaine en Robert Lang hebben aangetoond dat er nooit een efficiënt algoritme zal gevonden worden om een optimale stapel van cirkels te berekenen voor een rechthoekig stuk papier, wat zij betreuren want dit had handig geweest bij het tekenen van bepaalde vouwpatronen.
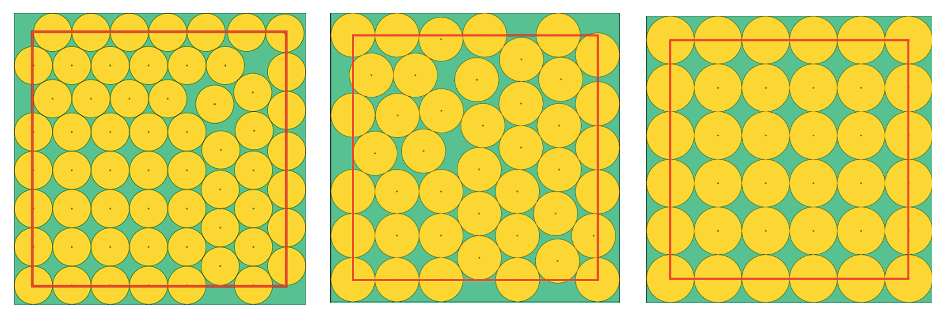
Als kleine toegift of dienstverlening voor de organisatoren onder jullie hebben we laten uitrekenen hoeveel toeschouwers we op een corona-veilige wijze kunnen plaatsen bij een ceremonie of podiumact in een ruimte van tien op tien meter, hieronder weergegeven door een rood vierkant. In de eerste oplossing kunnen we 59 stoelen zetten, in evenveel middelpunten van cirkels waarvoor een diameter van 1,5 m genomen werd. Dan is de tweede oplossing met 43 stoelen en een diameter van 1,8 m meer realistisch (schouderbreedte van 30 cm). Wie een nog grotere marge verkiest, kunnen we cirkels met een diameter van twee meter aanbevelen, waarvoor de computer onverwachts een vierkant raster van 36 stippen als oplossing heeft. Mooier hoeft het niet te worden voor ons.