Begin maart voorspelden "wiskundige modellen" van de covid-19-pandemie een meltdown van onze gezondheidszorg. Het gevolg was een lockdown om dat scenario te vermijden. Wiskundige Bert Mortier evalueert in deze blogpost de voorspellende waarde van die wiskundige modellen.
Als reactie op die voorspellingen, en op de ontwikkelingen in landen zoals Italië, hebben regeringen overal ter wereld hun heil gezocht in een strikte lockdown. Een voorbeeld van zo’n voorspelling door een wiskundig model staat getoond in de bovenstaande figuur. Zonder lockdown zou onze gezondheidszorg overrompeld worden.
Aangezien wiskundige modellen mee het beleid bepalen, is begrip van hoe een wiskundig model gebruikt kan worden onontbeerlijk. Om die reden bekijken we in deze tekst het meestgebruikte wiskundige model voor de verspreiding van infectieziektes. We passen dit model daarna toe op de specifieke situatie in België. Dit wiskundige model kan dan gebruikt worden om nog verder in de toekomst te kijken en voorspellen wat er gebeurt indien de lockdown plots zou ophouden.
Voorspelling van de epidemie
Het nieuwe SARS-CoV-2 virus nestelt zich in het ademhalingssysteem, waar het zich kan vermenigvuldigen, ten koste van de gastheer. De beschadigingen in het ademhalingssysteem van besmette personen leiden soms tot zware ziekte, COVID-19, maar meestal herstelt een besmet persoon, waarna die immuun wordt. Tijdens de besmettelijke periode kunnen de vele virusdeeltjes in het ademhalingssysteem van een besmet persoon terechtkomen in nieuwe, nog steeds vatbare personen door mee te reizen met druppeltjes in de adem van de besmette persoon. Daar kan het virus zich dan verder vermenigvuldigen. De epidemie voltrekt zich dan door een lange, steeds uitbreidende keten van contacten die resulteren in nieuwe besmettingen.
Het meest gebruikte wiskundige model voor epidemieën versimpelt de realiteit aanzienlijk. In plaats van reële contacten tussen mensen, wordt contact tussen mensen gemodelleerd alsof er tussen elke twee personen een gelijke kans is om contact te hebben. Als er een contact gebeurt tussen een besmet persoon en een vatbaar persoon, dan is er opnieuw een kans dat die besmetting wordt overgedragen. Het geneesproces wordt in dit model beschreven als een vaste kans per dag om te genezen.
De bovenstaande beschrijving van het model kan vertaald worden in wiskundige vergelijkingen die aangeven hoe het aantal nog steeds vatbare personen, aangeduid met V , het aantal besmette personen, aangeduid met B en het aantal herstelde en nu dus immune personen, aangeduid met I , veranderen. Deze aantallen veranderen doordat vatbare personen besmet worden door contact met andere besmette individuen, en doordat besmette personen herstellen. Deze veranderingen worden getoond in de onderstaande figuur.

Het model beschrijft deze veranderingen door, voor elk van die drie groepen personen, het aantal personen in die groep op de n -de dag voor te stellen als Bn , Vn en In . Het model beschrijft dan het aantal besmette, vatbare en immune personen op de volgende, (n+1) -e, dag aan de hand van de aantallen op de n -de dag. Om die evolutie te beschrijven, is ook de kans op een contact tussen twee mensen, κ , de kans op besmetting indien er contact is tussen een vatbare en een besmette persoon, α en de kans op genezing per dag, γ , nodig. Met deze kansen kunnen het aantal nieuwe besmettingen en het aantal herstelde personen wiskundig worden uitgedrukt. Hoe dit precies in zijn werk gaat wordt uitgelegd in de grijze kadertekst, voor de geïnteresseerden. In de onderstaande figuur staan deze veranderingen wiskundig aangeduid.

Daarmee kunnen de wiskundige vergelijkingen worden opgesteld voor het aantal besmette, vatbare en immune personen op de (n+1) -e, dag. Deze zijn:
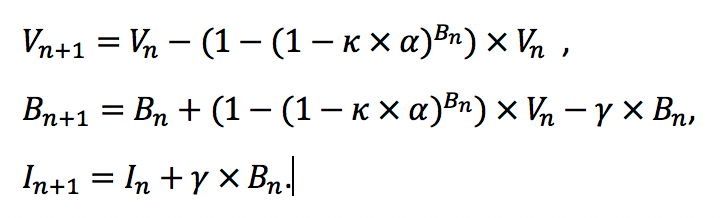

De bovenstaande vergelijkingen geven dan wel de manier waarop het aantal vatbare, besmette en immune personen evolueren, maar alvorens die te kunnen gebruiken, hebben we waarden nodig voor V , B en I op een bepaalde dag, alsook waarden voor de kansen κ , α en γ . Al heel vroeg in de epidemie waren er schattingen beschikbaar voor die kansen, namelijk γ=1/13 , κ×α=3,7×10-6 . Met die waarden kunnen we experimenteren. We kunnen bijvoorbeeld trachten te kijken naar hoe het aantal besmettingen zou evolueren in België, met een bevolking van 11.500.000 mensen, beginnende van één enkele besmetting. Dat betekent dat B1=1 , V1=11.499.999 en I1=0 . Deze waarden invullen in de vergelijkingen geeft een voorspelling van B2 , V2 en I2 . Deze nieuwe waarden opnieuw in de vergelijkingen invullen geeft dan B3 , V3 en I3 . Dit proces kan worden voortgezet tot we de waarden B365 , V365 en I365 kunnen berekenen, één jaar na het opduiken van een eerste besmetting.
Het resultaat van dit proces wordt getoond in de onderstaande figuur. Die leert ons dat de epidemie misschien traag op gang komt, maar na enkele maanden al zouden miljoenen mensen tegelijk besmet zijn.

De vraag stelt zich nu of dit een probleem is. Een initiële vergelijking deed uitschijnen dat de nieuwe ziekte niet veel schadelijker is dan de griep, maar wel een stuk besmettelijker is. Die vergelijking maakt het logisch om de ziekte beperkt te laten woekeren, zonder ons leven stil te leggen. Na verloop van tijd werd evenwel duidelijke dat de impact van het nieuwe coronavirus veel groter is. Het duurde tot de dramatische ontwikkelingen in Noord-Italië, tot er drastische maatregelen werden genomen doorheen Europa om de epidemie in te dijken. De impact van het virus op onze maatschappij kan in het wiskundige model worden opgenomen, bijvoorbeeld door het aantal ingenomen intensieve zorgen bedden mee te modelleren. We duiden het aantal bedden op intensieve zorgen (IZ) aan met Z . Er is namelijk data beschikbaar die stelt dat ongeveer 0,82 % van de besmette personen een IZ bed vereist. We kunnen dat wiskundig beschrijven door te stellen dat
Zn=0,0082×Bn .
De evolutie van het aantal vereiste IZ bedden kan eenvoudig worden gevonden in de vorige figuur. Die evolutie staat getoond in de onderstaande figuur. De zwarte lijn duidt de maximumcapaciteit aan IZ bedden in België. Deze grafiek illustreert wel heel erg duidelijk dat er zich een ramp zou voltrekken indien het virus niet kon worden ingeperkt.
Zo’n uitkomst van het model noopt aan tot heel grote actie. Dit is echter enkel duidelijk nadat de zware impact op de gezondheidszorg ook was opgenomen in het model. Dit mag niet uit het oog verloren worden bij modelleren: als de correcte oorzaak niet is opgenomen, kunnen de conclusies niet juist zijn. Een tweede aspect is dat de voorspellingen door het model niet meer detail en precisie bevatten, dan het model zelf. Zo is de gemodelleerde vorm van contact een heel simplistische aggregatie van de realiteit, en de voorspellingen zullen dan ook niet erg nauwkeurig zijn. Het enige dat het model kan, is benaderend voorspellen hoe de epidemie als geheel ongeveer zou evolueren. Naast de fikse vereenvoudigingen in het model, komt de precisie ook in het gedrang doordat de waarden van κ , α en γ bepaald werden via de beperkte data die beschikbaar is.
Zelfs al zit het model er ver naast, en is het maximaal aantal nodige IZ bedden niet 30.000, maar ‘slechts’ 10.000, dan nog houdt de conclusie stand: als er niets zou veranderen, komt er een enorme overrompeling van ons gezondheidssysteem.
Vergelijking met de realiteit
We kunnen het bovenstaande wiskundige model gebruiken om algemene voorspellingen te maken dankzij gegevens uit het buitenland over de ziekte en diens verspreiding. Deze gegevens werden gebruikt om de waarden van κ , α en γ te bepalen. Hoe de pandemie precies in België verliep, verschilt van de hierboven gemaakte aannames. Het was namelijk niet zo dat de epidemie in België begon met 1 besmet individu, en ook de ingevoerde lockdown heeft een enorm verschil gemaakt.
We kunnen een connectie maken tussen het simpele wiskundige model en de Belgische realiteit aan de hand van drie zaken. Ten eerste is er een initieel aantal besmettingen van waaruit vertrokken wordt, bijvoorbeeld het aantal op 1 maart. Ten tweede is er de mate waarmee het aantal contacten en de kans op besmetting tijdens die contacten is afgenomen na de lockdown. Dit bepaalt een verandering van κ×α vanaf de lockdown. Ten slotte is er een bepaalde periode van aanpassing geweest, waarin het effect van de maatregelen langzaamaan zichtbaar werd. Deze drie zaken worden gevat in drie getallen: B1 is het aantal besmette personen op 1 maart, β is de factor waarmee κ×α is afgenomen en T is de aanpassingstijd waarna het effect van de maatregelen pas echt compleet was.
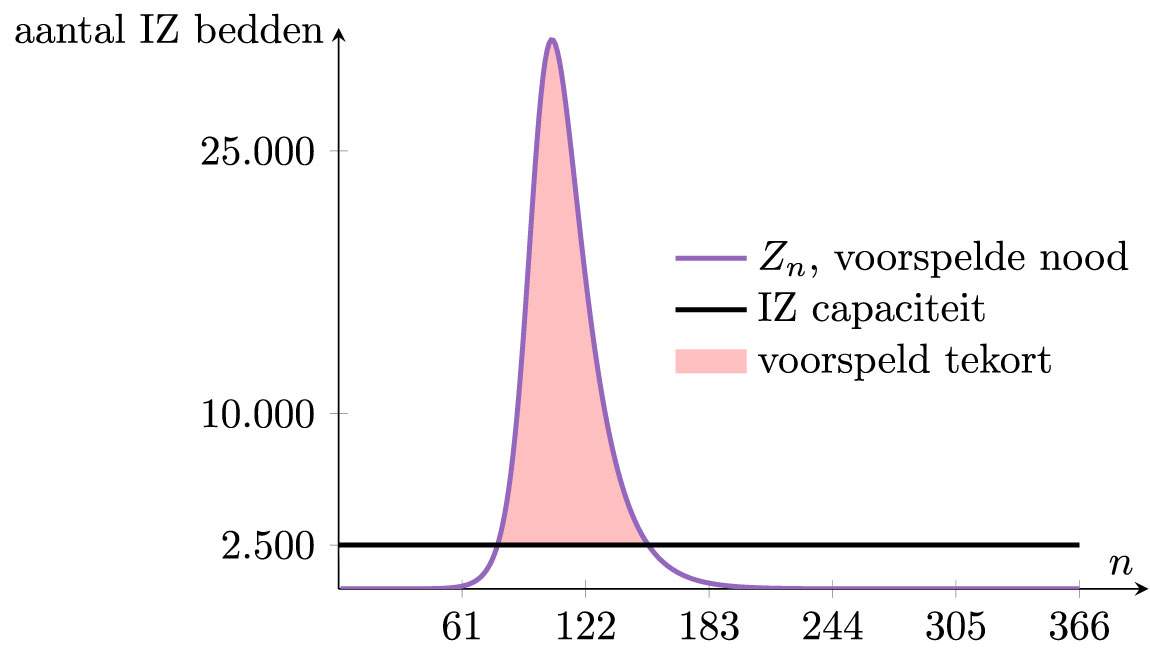
Deze drie getallen, B1 , β en T zijn onbekend, en we zullen ze kiezen zodat het model overeenstemt met de Belgische realiteit. Dit verloopt via een zogenaamde model-fit. Het blijkt dat de beste keuze is dat er op 1 maart 1.000 besmettingen waren (B1=1.000) , dat de lockdown het aantal contacten en resulterende overdragingen met een factor 8 deed afnemen (β=8 ), en dat het zo’n 30 dagen duurde alvorens het effect volledig was (T=30 ). Met deze keuzes komt de uitkomst van het voorspelde ingenomen aantal IZ bedden heel goed overeen met de Belgische realiteit.
We hadden al een model, maar nu hebben we ook een model dat ‘werkt’ voor België. We kunnen nu verdere voorspellingen maken van hoe de epidemie in België zou verlopen.
Een nieuwe blik op de toekomst
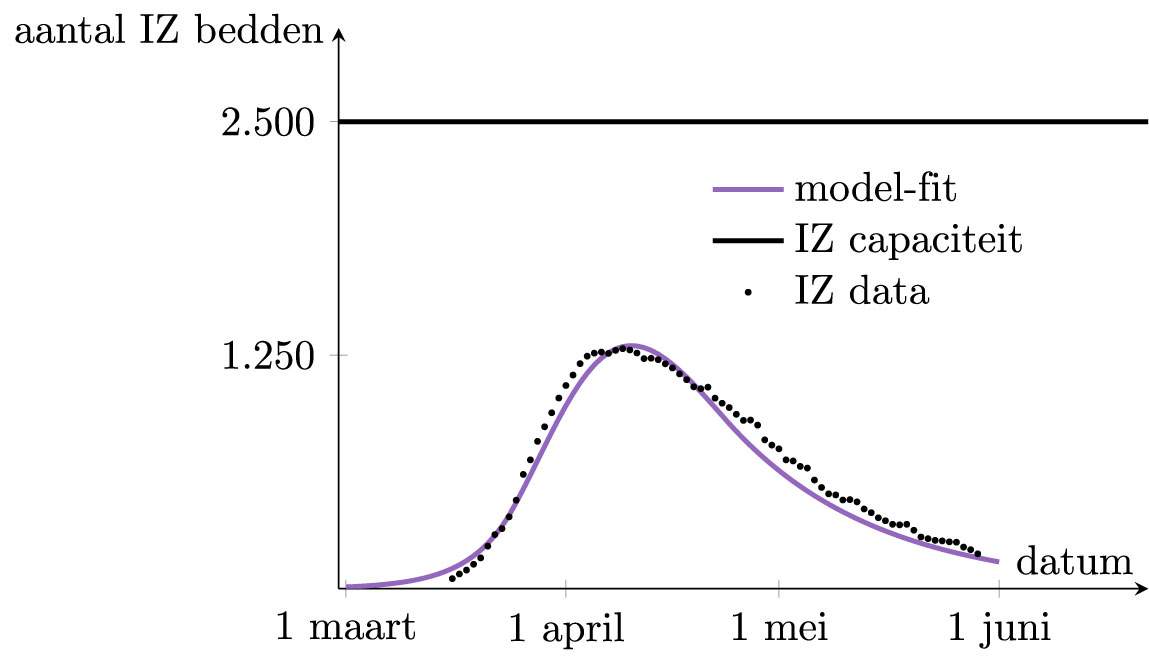
We kunnen het wiskundige model bijvoorbeeld gebruiken om te voorspellen wat er zou gebeuren in België als alle maatregelen zouden beëindigd worden op 1 juni. Dit kan worden opgenomen in het wiskundige model door vanaf 1 juni de waarden van κ , α en γ terug te brengen naar de oorspronkelijke waarden. Het resultaat zie je hier onder, en het zou nog steeds een ramp zijn. Deze voorspelling leert dus dat het volledig opheffen van de maatregelen niet kan zolang er geen vaccin of bredere immuniteit is. De aanname dat alle maatregelen op 1 juni werden opgeheven in België is echter niet volledig juist. Zo zijn er gedurende heel de zomer nog restricties op het samenkomen in grote groepen, zijn grote evenementen haast overal afgeschaft en worden mondmaskers op meerdere plaatsen verplicht. Het is dus te verwachten dat de stijging in realiteit niet zo extreem zal zijn als in de onderstaande grafiek.
Hoe groot het effect van al die overblijvende maatregelen is, zal nog moeten blijken. Merk ook op dat er heel wat vertraging kan zitten tussen het opheffen van de maatregelen en het zichtbaar worden van een stijging in de grafiek. In het voorbeeld hierboven, waarbij de lockdown volledig werd opgeheven op 1 juni, duurt het tot midden augustus alvorens de vraag naar IZ bedden weer duidelijk stijgt. Eens het begint te stijgen, duurt het evenwel niet lang alvorens de situatie weer precair wordt. Het kan dus zijn dat er heel plots een nieuwe lockdown nodig zal zijn.
Hoe accuraat de voorspellingen door het wiskundige model precies zullen blijken te zijn, is steeds koffiedik kijken. Er is hierbij een enorm verschil tussen de model-fit met de Belgische IZ data, die haast perfect was, en de toekomstvoorspellingen voor wat er zou gebeuren indien er geen lockdown meer is. De grote overeenkomst tussen de IZ data en het model ontstaat doordat de waarden B1 , β en T precies zo gekozen worden dat de curve goed overeenkwomt. Voor toekomstige waarden kan die truc niet gebruikt worden en de accuraatheid van toekomstvoorspellingen hangt dus af van de accuraatheid van het model, wat onzeker is. Om het met een boutade te zeggen: modellen zijn vooral enorm goed in het verleden te voorspellen, in de toekomst voorspellen een stuk minder.
Als er fouten in de voorspellingen blijken te zitten, kan het model worden aangescherpt, bijvoorbeeld door extra effecten in rekening te brengen. Zo kan in acht genomen worden dat het virus zich beter of slechter verspreidt afhankelijk van het weer, of menselijke contacten kunnen beter worden beschreven in het wiskundige model. In de realiteit zijn onze contacten namelijk niet volkomen willekeurig: we komen meer in contact met mensen die dicht wonen, of op dezelfde plek werken, enzovoort. Al deze extra aspecten kunnen gevat worden in nieuwe wiskundige modellen. Opdat die aspecten accuraat weergegeven worden, zullen gegevens nodig zijn. Zo zijn er gegevens nodig over het gemiddeld aantal contacten met buren, collega’s en familie, en hoe groot de kans op besmetting bij die verschillende soorten contacten is. Als er betrouwbare data is om die gegevens te bepalen, kan het wiskundige model steeds betere voorspellingen geven.



