Geen fans in het stadion, maar wel miljoenen kijkers thuis voor de buis om de openingsceremonie van de 32e Olympische Spelen in Tokyo te volgen. Zoals steeds een hele show, waarbij de Japanners deze keer uitpakten met onder meer een technisch hoogstandje met 1824 drones. Maar de eerste halve minuut van het spektakel was al meer dan genoeg om onze wiskundige honger weer voor even te stillen.
In den beginne was er niets. En uit dat niets ontstond alles. Alles wat we rondom ons kunnen waarnemen, maar uiteraard ook meer dan dat (denk maar aan de wiskunde zelf: niet expliciet waar te nemen, maar bestaan doet ze zeker). Wie of wat de oorzaak daarvan is, daar kan men oeverloos over filosoferen, maar voor een wiskundige is deze schepping niets anders dan het verhogen van de dimensie: van het nuldimensionale niets naar onze driedimensionale wereld.
De beginanimatie van de olympische openingsceremonie toont ons deze wondermooie wiskundige creatie. Een punt heeft namelijk per definitie geen lengte, breedte of hoogte. We noemen een punt dan ook nuldimensionaal (0D). Voegen we een dimensie toe, dan krijgen we een lijn of, als we daar een deeltje van nemen met een bepaalde lengte, een lijnstuk (1D). Een vlak, of een deel van het vlak met een zekere lengte en breedte zoals het getoonde vierkant, is dan weer tweedimensionaal (2D). Doen we er tot slot een hoogte bij, dan krijg je een kubus in de driedimensionale ruimte rondom ons (3D). (Wiskundigen en fysici stoppen hier niet, voor hen zijn 4, 5 of zelfs oneindig veel dimensies quasi dagelijkse kost, maar voor de elementaire meetkunde volstaan 3 dimensies.)
Vervolgens zoomen we uit op de kubus, en krijgen we maar liefst 12 in het rond zwevende ruimtelichamen te zien. We overlopen ze een voor een, en vertellen waarom deze lichamen, althans in onze bescheiden ogen, interessanter zijn dan die in de atletische betekenis van dat woord.

Beginnen doen we met de perfectie zelve: de bol (nr. 1), gedefinieerd als de verzameling van alle punten op een zekere afstand (de straal) van een gegeven punt (het middelpunt) in een driedimensionale ruimte. Perfectie zeggen we, maar perfecte lichamen bestaan natuurlijk niet in de realiteit. De aarde bijvoorbeeld lijkt van ver misschien wel een bol te zijn, maar is dat niet. Zelfs al laten we bergen, ravijnen en zeeën buiten beschouwing, dan nog zorgt de draaiing rond haar as voor een afplattend effect rond de polen, waardoor de aarde geen bol maar een soort ellipsoïde is. Ook in menig sport wordt natuurlijk gebruik gemaakt van een bal, maar zelden tot nooit zijn dit bollen. Een voetbal, een basketbal, een hockeybal, ...: allen benaderen ze zo goed en zo kwaad mogelijk een bol, maar echt perfect bolvormig zijn ze nooit. Vaak worden die maximale afwijkingen ook in reglementen gegoten, bijvoorbeeld bij (het niet-olympische) biljarten: daar mogen er putjes van maximaal 0,22% van de diameter in de bal zitten (bijvoorbeeld door slijtage door het spelen). Het reliëf van de aarde daarentegen, de hoogste berg of de diepste zee, heeft een kleinere afwijking ten opzichte van de gemiddelde diameter, namelijk zo'n 0,17%. Men kan dus zeggen dat de aarde in zekere zin gladder is dan een biljartbal. Misschien spelen de Griekse goden van Olympus binnenkort wel planetenbiljart in de eerste editie van de Intergalactische Spelen?
De volgende twee lichamen zijn enigzins verwant met de bol: de cilinder (nr. 2) en de kegel (nr. 3). Het verwantschap is natuurlijk te vinden via hun cirkelvormigheid en het getal $\pi$ dat opduikt in allerhande formules van oppervlaktes en volumes van deze lichamen. Zo geldt er bijvoorbeeld dat de oppervlakte van een bol met straal $r$ gelijk is aan $A = 4\pi r^2$, een formule die reeds door Archimedes gekend was. Opmerkelijk: de oppervlakte van een cirkel met dezelfde straal, die je zou kunnen zien als de schaduw van die bol als de lichtbron maar ver genoeg staat, is $\pi r^2$. Met andere woorden, de oppervlakte van een bol is precies vier maal die van zijn schaduw. Dat dat niet toevallig is, heeft alles te maken met een cilinder: de oppervlakte van de cilinder die juist rond de bol past (met andere woorden, met straal $r$ en hoogte $2r$), is ook juist $4\pi r^2$, tenminste als we de grondvlakken even negeren. De uitleg daarvan kan je in dit filmpje (in het Engels) terugvinden, inclusief animaties waarom dit dan precies ook die 4 cirkels zijn.
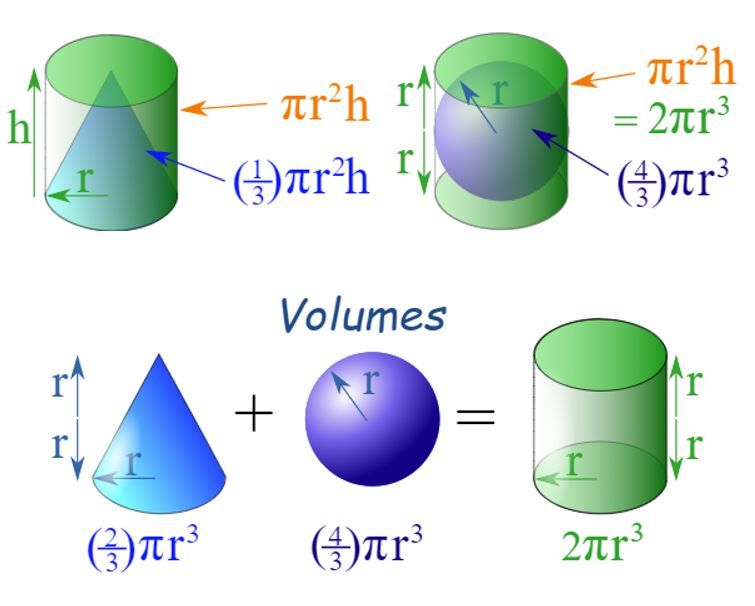
We verlossen u ook graag van uw nieuwsgierigheid naar een mooi verband met de kegel: als je tegelijkertijd ook nog een zo groot mogelijke kegel in diezelfde cilinder past, dan blijkt dat het volume van de kegel plus het volume van de bol precies gelijk is aan het volume van de cilinder. De pracht van wiskunde blijft verbazen!
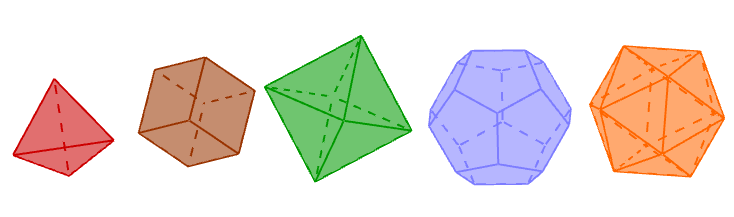
Op naar een nieuwe categorie binnen onze olympische lichamen, namelijk nrs. 4 tot en met 8: de zogenaamde platonische lichamen, vernoemd naar de Griekse filosoof Plato, en ook gekend als de regelmatige veelvlakken. Ze bestaan telkens uit een aantal regelmatige drie-, vier- of vijfhoeken, allemaal van dezelfde grootte, zodat in elk hoekpunt juist evenveel vlakken samenkomen. Ze worden genoemd naar het aantal vlakken (in het Grieks) die ze bevatten: respectievelijk de tetraëder (4 driehoeken), de hexaëder of kubus (6 vierkanten), de octaëder (8 driehoeken), de dodecaëder (12 vijfhoeken) en de icosaëder (20 driehoeken). Dat er juist vijf van deze lichamen zijn, werd reeds bewezen door Euclides rond 300 v.Chr, en is niet zo heel moeilijk om in te zien.
Stel dat we zo een veelvlak willen bouwen, laat ons dan eens kijken naar een willekeurig hoekpunt. Daar komen minstens drie vlakken samen (twee vlakken die samenkomen, doen dat in een zijde of ribbe, niet in een hoekpunt), en de som van de hoeken van die veelhoeken is kleiner dan 360° (want als die gelijk is aan 360° krijg je een plat vlak, wat we natuurlijk niet willen). De hoeken in een regelmatige driehoek zijn 60°, dus we kunnen er 3 (3 x 60° = 180°), 4 (240°) of 5 (300°) samenvoegen. Vanaf 6 zitten we aan die grens van 360° die we niet mochten overschrijden. Voor regelmatige vierhoeken (vierkanten dus) is er maar een optie, namelijk 3 x 90° = 270°. En ook bij regelmatige vijfhoeken is er slechts een mogelijkheid binnen onze grenzen: 3 x 108° = 324°. Andere mogelijkheden zijn er dus niet (reken zelf maar eens uit).
Deze vijf regelmatige veelvlakken werden door veel wiskundigen en wetenschappers doorheen de geschiedenis bestudeerd. Pythagoras wist bijvoorbeeld reeds 200 jaar voor Plato en Euclides van het bestaan van 3 van de 5 af: de tetraëder, kubus en dodecaëder. Plato linkte de vijf lichamen aan de vijf kosmische bouwstenen van het heelal: water, aarde, lucht, vuur en hemelmaterie. Een kleine 2000 jaar later was het Kepler die ze rond het jaar 1600 in zijn eerste boek met de structuur van het zonnestelsel in verband bracht, met name de vijf planeten (naast de aarde) die toen bekend waren. In de natuur komen de tetraëder, kubus en octaëder voor als kristalstructuren, en ook virussen en bepaalde chemische moleculen nemen soms de vorm aan van een van deze vijf lichamen. Fans van bordspellen komen de vijf regelmatige veelvlakken geregeld tegen in hun dobbelsteenverzameling, en ook de bekende Rubiks Kubus is verkrijgbaar in de vier andere platonische vormen, al bestaan er in beide gevallen ook nog andere vormen die geen regelmatige veelvlakken zijn.

Met behulp van deze vijf regelmatige veelvlakken kunnen we de volgende categorie van onze olympische lichamen vormen. Nummer 9 is namelijk een samenvoegsel van twee gelijke tetraëders, nummer 10 is de combinatie van een kubus en een octaëder, en (iets moeilijker te onderscheiden op bovenstaande figuur) nummer 11 is een dodcaëder doorheen een icosaëder. Dat het juist die combinaties zijn, is ook geen toeval: dit zijn namelijk de duale paren binnen de platonische lichamen. Deze duale paren bezitten een bijzondere verwantschap: neem een kubus, duid de middelpunten van de zes zijvlakken aan, en verbind deze. Je krijgt een (weliswaar kleinere) octaëder. En vice versa: de middelpunten van de zijvlakken van een octaëder leveren een kubus op. Ook voor het duo dodeca- en icosaëder geldt dit. En de tetraëder is, raar maar waar, haar eigen duale lichaam.
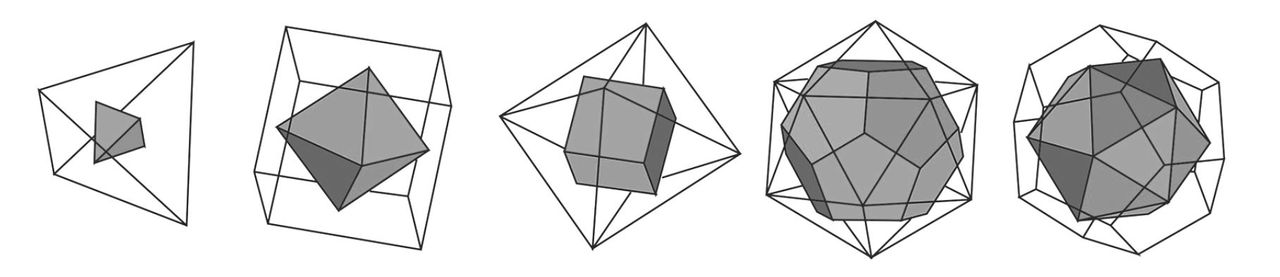
Als je nu zo'n duaal paar neemt, en je vergroot de binnenste van de twee net zo veel tot de ribben van beide elkaar juist snijden, dan krijg je de combinaties uit de openingsceremonie.

Er is nog een andere manier om deze lichamen te bekomen vanuit de regelmatige veelvlakken, maar daarvoor hebben we het begrip versterring (in het Engels: stellation) nodig. Om dit te verduidelijken, keren we even terug naar een dimensie lager, met name naar de wereld van de veelhoeken. De bekendste versterring is een pentagram: neem een regelmatige vijfhoek, en trek alle zijden verder door tot ze elkaar terug snijden. Hetzelfde kan je doen met een zeshoek, je krijgt dan een hexagram. Voor een zevenhoek (alsook voor een achthoek) heb je zelfs twee mogelijke versterringen: de tweede krijg je namelijk door de eerste verder te versterren. Voor een negenhoek zijn dat er al drie, en dat gaat zo maar door. (Voor een driehoek of een vierhoek lukt dit niet. Waarom niet? Probeer het maar eens!)
Hetzelfde proces kan je doen met veelvlakken, maar dan door de zijvlakken uit te breiden tot ze elkaar opnieuw snijden. Het is ietwat moeilijker om in te beelden, laat staan dit via een duidelijke tekening voor te stellen, dus je zal ons hier op ons woord moeten geloven: vertrek je van een octaëder, dan krijg je door versterring het lichaam nr. 9, ook gekend onder de naam stella octangula (Latijn voor achtpuntige ster). Ook nr. 10 en 11 kunnen door versterring worden bekomen, zij het niet door te vertrekken van een platonisch lichaam maar wel van een bepaald archimedisch lichaam: nr. 10 is de eerste versterring van een kuboctaëder, en nr. 11 de eerste van een icosidodecaëder. Dergelijke ruimtelichamen komen trouwens geregeld voor in de werken van de bekende Nederlandse kunstenaar M.C. Escher. Voor de creatieveling nog dit: de stella octangula kan je met behulp van deze origami-tutorial ook zelf bouwen. Veel succes!
Tot slot hebben we nog nr. 12: te vinden als donut in menig bakker, als binnenband in menig stadsfiets, als servetring in menig horeca-etablissement of als koffiemok op het bureau van menig wiskundige. Dat laatste is wat men kan classificeren onder wiskundige humor. Het is namelijk zo dat in een bepaald deelgebied van de wiskunde, met name de topologie, twee objecten als gelijk worden beschouwd als je het ene kan boetseren uit het andere zonder te scheuren of te plakken. Een torus (want dat is de officiële wiskundige naam van figuur 12) en een koffiemok zijn voor topologen bijgevolg gelijk, zoals te zien is in deze animatie:

Net zoals de bol/bal-sporten waar we mee begonnen, komt ook dit laatste ruimtelichaam uit ons rijtje veelvuldig voor binnen de Olympische Spelen (de cirkel is met andere woorden rond): de basketbalring, de ringen bij het turnen, de vijf olympische ringen, ... (een boksring is hier echter geen goede vergelijking). Merk op dat de 12 lichamen (een subtiele verwijzing naar de 12 Griekse goden die op de berg Olympus wonen?) in de openingsceremonie zelf ook in een soort torus-formatie rondvliegen, alvorens we inzoomen op de torus zelf. Die verandert magischerwijze in het Olympische Stadion in Tokyo, waarna het live-gedeelte van de openingsceremonie in dat stadion van start kon gaan.




