Op 5 december is wiskundige Jacques Tits op 91-jarige leeftijd overleden. Hij was vooral bekend van de groepentheorie, waarvoor hij de Abelprijs ontving.
Wiskundige Dirk Huylebrouck schreef naar aanleiding van die prijsuitreiking dit artikel, dat in 2008 verscheen in Eos magazine.
Wiskundigen hadden in de vorige eeuw een werelds probleem: Alfred Nobel vond hen niet toegepast genoeg voor het ‘goed van de mensheid’ en had dus geen prijs voorzien. Daarom kwam er later een Fieldsmedaille, genoemd naar de Canadese wiskundige John Charles Fields. De medaille gold lange tijd als officieuze Nobelprijs, maar wordt maar om de vier jaar uitgereikt, en dan nog alleen aan wetenschappers die jonger zijn dan veertig. Sinds 1978 gold de Wolf Prize soms als een beter alternatief voor de nobele leemte, maar uiteindelijk losten de Scandinaven het probleem zelf op door een jaarlijkse Abelprijs in te voeren, goed voor 750.000 euro.
Dat gebeurt sinds 2003, een jaar na de viering van de tweehonderdste verjaardag van de geboorte van de Noorse wiskundige Niels Hendrik Abel (1802-1829). Wellicht moeten er nog wat jaren en prestigieuze namen aan de erelijst worden toegevoegd voor de prijs zich in de menselijk geest grift als wiskundige Nobelprijs. Abel-Nobel: het rijmt alvast mooi. Jacques Tits kreeg zowat alle onderscheidingen in de wiskunde, behalve de vermelde Fieldsmedaille, waarvoor hij net iets te oud bleek. En toch, was hij vroeg genoeg begonnen met de wiskunde. Geboren op 12 augustus 1930, in Ukkel (Brussel), gaf hij – om financieel rond te komen na de dood van zijn vader (eveneens een wiskundige) – al op dertienjarige leeftijd bijlessen aan jongeren die vier jaar ouder waren dan hijzelf. Jacques sloeg enkele schooljaren over, en op veertienjarige leeftijd was hij primus bij het toelatingsexamen voor ingenieur aan de Université Libre de Bruxelles (ULB). Hij kon zo de studies wiskunde aanvatten, om in mei 1950 op negentienjarige leeftijd zijn doctoraat te behalen. Tot 1964 bleef hij aan de ULB, waarna hij naar de Universiteit van Bonn verhuisde, en uiteindelijk, in 1973, naar het Collège de France in Parijs. Tits werd lid van academies in Frankrijk, de Verenigde Staten, België en Nederland, en kreeg eredoctoraten aangeboden door de universiteiten van Utrecht, Gent, Bonn en Louvain-la-Neuve. En dat allemaal voor het werken met groepen en het bedenken van gebouwen (zie kaderstuk).
Mooie toepassingen
Tits formuleerde zijn fundamentele stelling over de herkenning van ingewikkelde groepen via bepaalde gebouwen reeds in 1974, in een lijvig boek met alle details en uitwerkingen. Of de jury van de Abelprijs, net zoals die van de Nobelprijs in de fysica, ook wachtte op doorslaggevende toepassingen van Tits’ theorieën, is twijfelachtig. Hoe dan ook, die zijn er ondertussen wel: er zijn namelijk ook gebouwen die niet zozeer als modellen voor groepen worden gezien en toch onmisbaar bleken in de moderne meetkunde, en zelfs vertakkingen hebben tot in de codeertheorie.
Het gebeurt wel eens meer in de wiskunde dat een vinding interessanter wordt wanneer ze haar beoogde doel overstijgt (dat is ook het geval in andere wetenschappen, of, voorwaar, in de kunst). Net zoals sommige wasmachines vandaag het opschrift fuzzy logic dragen, verwijzend naar een soort wiskundige logica, is het denkbaar dat er binnen afzienbare tijd een nieuw label verschijnt op de CD-speler: Based on Tits buildings. Hoe dan ook, Jacques Tits zelf weet beter: ‘Het zijn niet de toepassingen die de wiskunde mooi maken, maar de wiskunde die de toepassingen mooi maakt.’
In België is de naam van Jacques Tits gekend en geliefd bij zijn vele ‘leerlingen’, zoals prof. em. Francis Buekenhout (ULB), Bernhard Mühlherr (ULB), Jean-Pierre Tignol (Louvain-la-Neuve), Hendrik Van Maldeghem (UGent), en bij de leden van hun onderzoeksteams. Ze zijn bijzonder blij met de toekenning van de Abelprijs aan Jacques Tits, niet in het minst omdat ze hem kennen als een immer vriendelijk man, zonder kapsones en met zin voor humor. Toen tijdens een les aan het Collège de France de helft van de verlichting niet werkte, grapte hij dat de donkere helft van het bord voorbehouden zou worden voor de fouten. En sinds Tits hebben vele wiskundigen een voorkeur voor hetzelfde nagerecht: tijdens een conferentiediner onderbrak de Abelprijswinnaar de (te) plechtige sfeer met een luide kreet: ‘Voor mij een mousse au chocolat!’
Tits’ groepen en gebouwen
Tits kreeg de Abelprijs voor ‘zijn diepe verwezenlijkingen in de algebra en in het bijzonder voor zijn vormgeving van de moderne groepentheorie’. Een wiskundige ‘groep’ is een structuur die best heel abstract mag zijn. De 'gewone' gehele getallen 0, 1, -1, 2, -2... vormen ‘een wiskundige groep’, samen met de gebruikelijke optelling: met andere woorden, eenmaal de basisrekenregels gekend zijn, verloopt alle rekenwerk binnen dat kader.
Het kan echter nog abstracter. Beschouw een driehoek ABC en twee bewerkingen: ‘a’, de spiegeling om de zwaartelijn door A, en ‘b’, de draaiing over 120° in tegenwijzerzin.
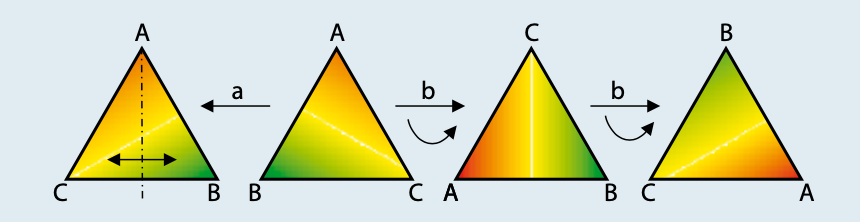
De bewerkingen a en b
De opeenvolging van twee bewerkingen heet dan de ‘samenstelling’, en speelt de rol van de optelling bij de gehele getallen. Samen met de bewerking ‘n’, ‘niets doen’, vormen a en b dan een ‘groep’. Het reken- of speelwerk kan beginnen, al stellen we snel vast dat een aantal ‘reken’-regels anders verlopen dan bij de gehele getallen: zo is ‘a na niets anders dan n, net zoals ‘b na b na b’/ Dat kan met de gebruikelijke notaties van kwadraten en derde machten worden aangeduid: ‘a na a’ = aa = a2 = n; analoog: b3=n. Wel is ‘a na b’ nu niet meer gelijk aan ‘b na a’ (ab =(ab ≠ ba), terwijl bij gewone gehele getallen natuurlijk wel ‘2+3 = 3+2’ geldt.
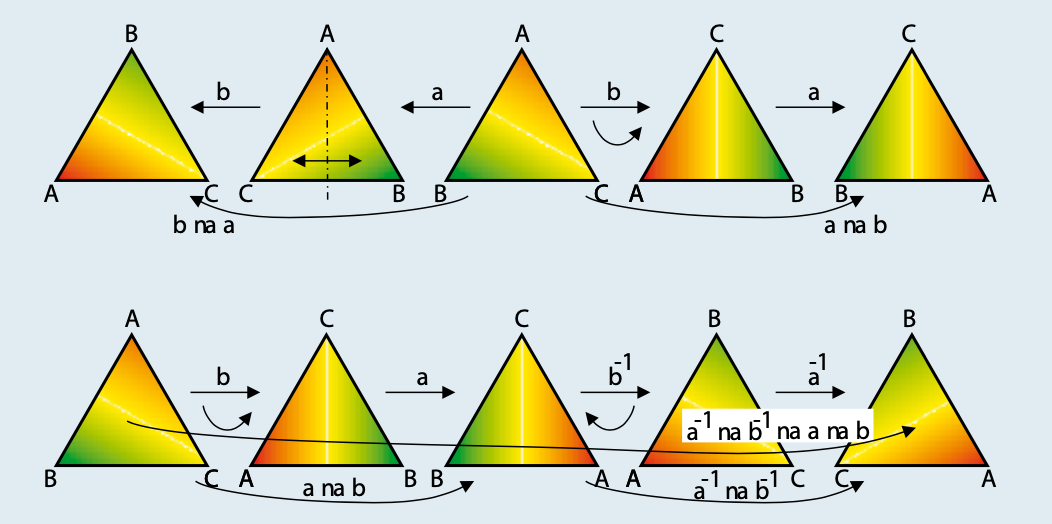
Twee rekenoefeningen in een ‘groep’: ab ≠ ba (boven), en a-1b-1ab = b2 (onder).
Sommigen zien dit snel in, net zoals sommigen bijzonder snel een Rubikkubus kunnen oplossen (en dat is eigenlijk ook groepentheorie). Wiskundigen werken zo dikwijls met deze groepen, dat zij in het geval van het voorbeeld niet meer denken aan een driehoek die wordt gedraaid en gespiegeld, maar deze groep van bewerkingen zien als een abstractie van die gelijkzijdige driehoek. Het is een beetje zoals wanneer men leert tellen: in het begin telt men 2 koeien en 3 koeien op, maar beetje bij beetje abstraheert zich dat tot 2 + 3. Een kristal wordt dan bijvoorbeeld niet meer door zijn precieze afmetingen beschreven, maar door de ‘groep’ die eraan wordt geassocieerd. Die abstractie heeft een groot voordeel, want net zoals het er bij het tellen niet meer toe doet of nu koeien of appels worden opgeteld, doet het er in de groepentheorie niet toe of er nu met driehoeken, kristallen, natuurkundige grootheden of huwelijksvoorschriften wordt gerekend.
Een ingewikkelder voorbeeld van een groep wordt voortgebracht door bewerkingen a en b die voldoen aan de volgende verbanden:
n = a2 = b3 = (ab)13 = (a−1b−1ab)5 = (a−1b−1 a−1b−1abab)4 = (abababa- bab−1)6.
De ‘n’ staat weer voor de operatie 'niets doen', zodat de eerste verbanden, a2 = n en b3 = n, doen denken aan de wetten die ook golden bij het spiegelen en draaien van een driehoek. De volgende uitdrukking met de dertiende macht van ab, toont echter dat het hier toch om iets anders schijnt te gaan. Jacques Tits slaagt er wonderwel in om zich in te beelden hoe in deze ‘groep’ gerekend kan worden, in zoverre zelfs dat hij vandaag de ‘Titsgroep’ heet.
De bekendste creatie van Tits is zijn ‘gebouwentheorie’, die toelaat om abstracte groepen te begrijpen. De benaming werd ingegeven door de verdere indeling van de structuur in ‘appartementen’ en in ‘kamers’. Een opeenvolging van kamers met vele gemeenschappelijke delen heet dan een ‘galerij’, maar verder is elke verwijzing naar vastgoed louter toevallig. Jacques Tits was ertoe gekomen via de studie van de zogenaamde ‘Lie-groepen’, genoemd naar Sophus Lie, een andere beroemde Noorse wiskundige uit de 19de eeuw. Tits merkte op dat de Lie-groepen deelgroepen bevatten met sterke eigenschappen, de zogenaamde ‘regelmatige veelvlakken in hogere dimensie’. Hij veralgemeende dat begrip, en later werden zijn ‘veralgemeende polytopen’ herdoopt tot ‘gebouwen’, en de bijzondere gevallen tot ‘appartementen’.
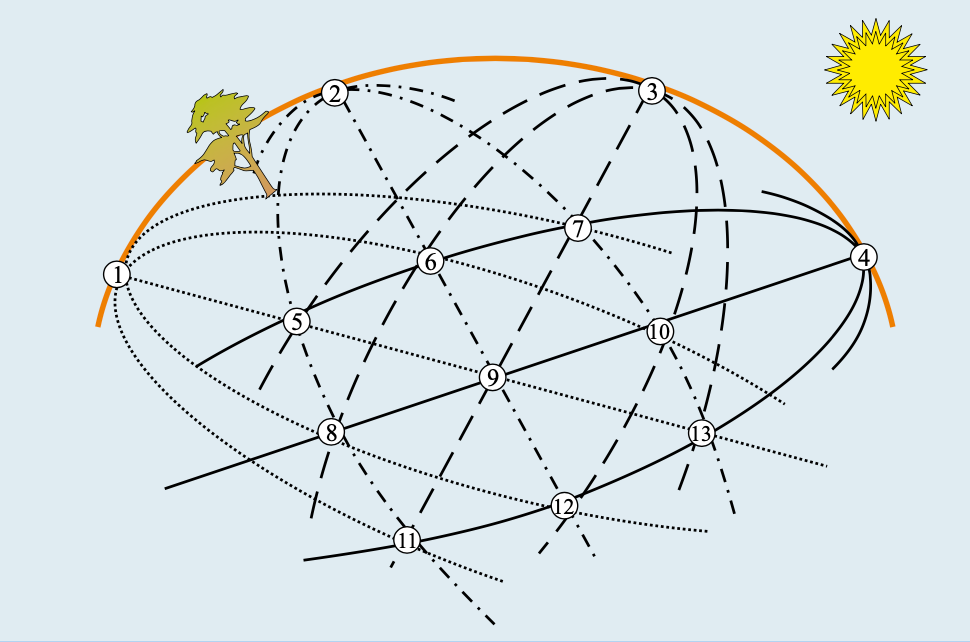
Bij het ‘eindig projectieve’ vlak van orde 13 bestaat het Titsgebouw uit de 13 punten 1, 2 ... 13 en 13 rechten 1-5-9-13, 1-7-8-12, 1- 11-6-10, 2-3-8-11 ... 1-2-3-4 (de ‘horizon’); de appartementen zijn driehoeken, zoals driehoek 10-4-13; de kamers zijn de paren gevormd door een rechte en een punt van die driehoek op die rechte, zoals het paar gevormd door de rechte 10-4-9-8 en het punt 4.
Een doorsnee Titsgebouw is veel complexer, maar de formele definitie van een Titsgebouw omhelst soortgelijke meetkundig klinkende basiswetten: twee kamers moeten steeds in een appartement liggen, terwijl twee appartementen steeds bepaalde delen gemeen moeten hebben. De grote verdienste van Tits was dat hij kon aantonen dat bepaalde ingewikkelde Liegroepen herkend konden worden door de aanwezigheid van bepaalde soorten gebouwen. Zijn behandeling van de ‘Liegroep E8’ staat bekend als de ‘constructie met het magische vierkant’, en dat is van belang in de natuurkunde, want de groep speelt een rol in de ‘Theorie van Alles’. Die ‘unificatietheorie’, een droombeeld van Albert Einstein, poogt de verschillende theorieën uit de natuurkunde te ‘groeperen’, zodat de gedragingen van elementaire deeltjes, de fundamentele natuurkrachten en de grootste sterrenstelsels in één model zouden passen. Maar deze Rubikkubus van het universum heeft zelfs Tits nog niet opgelost.



