Je staat in een televisiestudio voor drie gesloten deuren. Achter een van deze deuren staat een gloednieuwe auto en achter de andere twee een geit. Welke deur maak je open?
Wanneer de auto achter jouw gekozen deur staat, word jij de nieuwe eigenaar. Je twijfelt even en kiest dan voor deur 1. De presentator, die weet wat er achter elke deur zit, opent echter niet jouw gekozen deur, maar een andere waar een geit achter staat. Vervolgens vraagt hij jou: ‘Blijf je bij je oorspronkelijke keuze of wissel je naar de andere nog gesloten deur?’ Wat zou jij doen?
Dit is het beroemde Monty Hall-probleem, genoemd naar de presentator van het Amerikaanse televisieprogramma Let’s Make a Deal uit de jaren 1960. Blijf je bij je eerste keuze of wissel je naar de andere deur? De meeste mensen, misschien ook jij, denken dat het niet uitmaakt of je wisselt of niet. Na het openen van een deur met een geit, blijven er immers twee deuren over. Het lijkt alsof de kans op het winnen van de auto nu 50-50 is. Dit lijkt logisch, maar het klopt niet. De waarheid is dat je je kansen om de auto te winnen verdubbelt als je wisselt van deur. Deze strategie kan je verrassen en laat zien hoe je intuïtie je in de steek kan laten wanneer het om kansen draait.
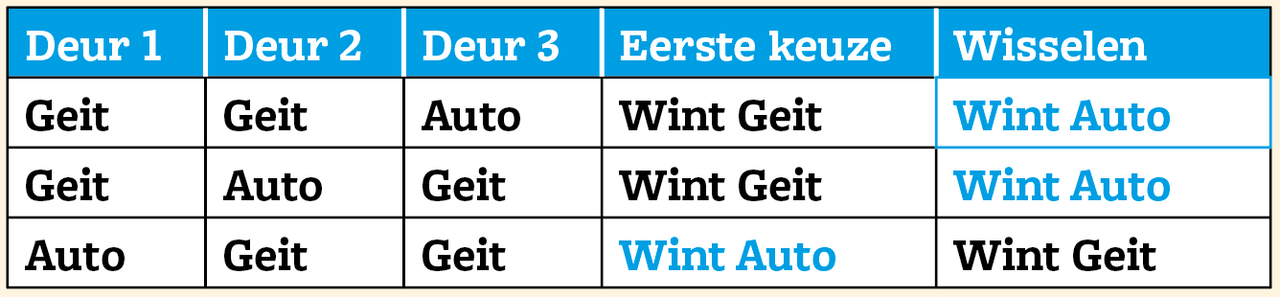
Hoe werkt het dan? Laat ons alle mogelijkheden waar de auto kan staan oplijsten, samen met het gevolg wanneer je bij je keuze van deur 1 blijft en wanneer je wisselt nadat de presentator een deur met een geit opende. De kans dat de auto achter deur 1 staat, is 1/3 wat betekent dat de kans dat de auto achter een van de andere twee deuren staat 2/3 is. De informatie die je van de presentator krijgt over deuren 2 en 3, laat je toe van deze kans gebruik te maken, zoals je in de tabel kan zien. Wie dus bij zijn initiële keuze blijft, heeft 1 kans op 3 om de auto te winnen, maar wie wisselt, heeft 2 kansen op 3!
De wisselstrategie zorgde zelfs voor een heuse controverse in de jaren 1990. Marilyn vos Savant, de vrouw met het toen hoogste IQ ooit gemeten, had een column in een bekend magazine waarin ze lezersvragen beantwoordde, waaronder de vraag naar de beste strategie bij het driedeurenspel. Ze schoof de wisselstrategie naar voor, maar lezers vonden het echter zo tegenintuïtief dat ze massaal in de pen kropen. Zo ontving ze een tienduizendtal brieven, ook van academici, waarin ze beticht werd van een denkfout. Vos Savant had het echter bij het rechte eind.
Hoewel het Monty Hall-probleem misschien zinloos lijkt in de echte wereld, illustreert de impact van de voorkennis van de presentator perfect hoe voorzichtig we moeten omspringen met informatie bij het nemen van beslissingen. Gelukkig biedt de kansrekening hier een kompas. De zogenaamde Regel van Bayes, beschreven in een essay uit 1763 van de Britse statisticus Thomas Bayes, helpt ons om te navigeren tussen kansen in situaties met voorkennis die veel complexer zijn dan het Monty Hall-probleem. Zijn regel wordt dagelijks gebruikt in verschillende sectoren van financiën en geneeskunde tot kunstmatige intelligentie, waar beslissingen vaak gebaseerd zijn op kansen en onzekerheid.
Laat me nog een voorbeeld geven over extra informatie die we niet altijd intuïtief meenemen, maar waarvan de impact dankzij Bayes zichtbaar wordt. Stel dat er in jouw regio in 2 procent van de tuinen een exotische orchidee bloeit. Je denkt de gelukkige eigenaar te zijn van zo’n exemplaar en downloadt een app die claimt om met 95 procent zekerheid zo’n orchidee te herkennen wanneer je er een foto van maakt en met slechts 3 procent kans een andere bloem foutief als orchidee te bestempelen. Je maakt een kiekje van de bloem en de app zegt dat je prijs hebt. Hoe groot is de kans dat het écht die zeldzame bloem is? Intuïtief denk je 95 procent, toch? De app is immers superaccuraat, niet?
Bayes zegt echter dat wat de app zegt, moet afgewogen worden tegen dat wat we weten, namelijk dat zulke orchideeën zeldzaam zijn. De kans dat de app ja roept, valt namelijk uiteen in twee scenario’s: het is een echte orchidee of het gaat om een andere bloem en je kreeg dus een foute melding. Het eerste doet zich voor met kans 0,95 × 0,02 = 0,019, het tweede met kans 0,03 × (100-0,02) = 0,0294, waardoor de kans op een echte orchidee bij een positief antwoord neerkomt op 0,019 / (0,019 + 0,0294) ≈ 0,39 of 39 procent. Geen 95 procent en zelfs niet eens de helft ervan. Dit omdat de zeldzaamheid van de orchidee de kans op een juist antwoord significant omlaag trekt, hoe slim je app ook is.
Zet dus soms je intuïtie even opzij en leer denken als een wiskundige.



