Wat is het verband tussen de beurskoers, de foto’s op jouw computer en een kartonnen doos? Ogenschijnlijk nutteloos wiskundig onderzoek.
“Monsterlijk” en “een aanfluiting van het gezonde verstand”. Zo omschreven tijdgenoten van de Duitse wiskundige Karl Weierstrass zijn oplossing van een probleem over het gedrag van wiskundige functies. Die mocht dan wel theoretisch volledig correct zijn, ze druiste jammer genoeg in tegen alle intuïtie. Maar honderd jaar later, toen Weierstrass allang dood was, bleek dat zijn oplossing verrassend sterk leek op het gedrag van de beurskoers en probeerden mensen het daarmee te voorspellen.
Weierstrass' wiskundige functie (links) bleek 100 jaar later van pas te komen om de beurskoers (rechts) te voorspellen.
Het verhaal van Weierstrass is niet het enige over theoretisch onderzoek dat pas later tot toepassingen leidt. Zo hebben we lichte maar stevige kartonnen dozen te danken aan een andere Duitse wiskundige, Carl Friedrich Gauss, en zijn werk over kromming begin negentiende eeuw. Ook de studie van meetkunde in oneindig veel dimensies begon als theoretisch onderzoek, maar heeft 80 jaar later, dankzij het werk van de Belgische wiskundige Ingrid Daubechies, een van de standaard bestandsformaten opgeleverd waarin je de foto’s op je computer bekijkt.
Puzzelen aan onze kennis
Onderzoek kun je zien als het leggen van een puzzel. Of het nu gaat over onderzoek in geneeskunde, geschiedenis of wiskunde – het blijft puzzelen, en onderzoekers leggen een grote diversiteit aan puzzels. Die puzzels kunnen concrete problemen uit de echte wereld oplossen of specifieke gaten in de kennis van een vakgebied opvullen, hoe abstract of theoretisch die gaten ook zijn.
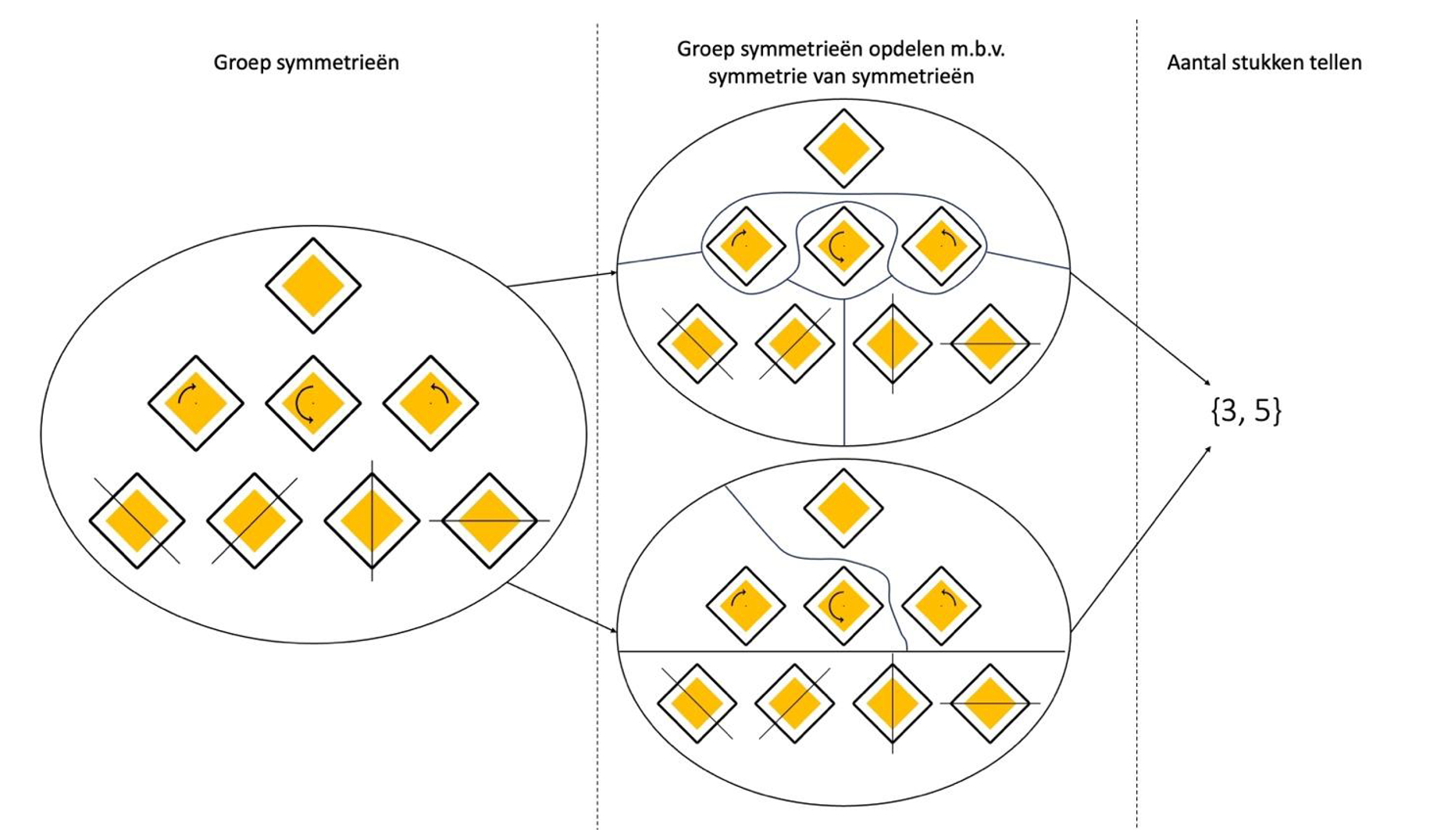
De drie lagen van mijn onderzoek: de groep symmetrieën van het verkeersbord, de symmetrieën van die groep symmetrieën en de gekoppelde verzameling getallen.
De meeste puzzels in de zuivere wiskunde behoren tot de tweede categorie en dat is ook bij mijn onderzoek het geval. Mijn puzzel vertrekt van de symmetrie van bepaalde vormen, zoals een cirkel, een kubus of een vierkant. Stel je bijvoorbeeld het wit-oranje verkeersbord voor. Zoals je op de figuur ziet, kun je het naar rechts of links draaien, of spiegelen rond een verticale, horizontale of schuine as, zonder dat de vorm verandert. Zo’n handeling – draaien of spiegelen zonder dat de vorm verandert – noemen we een symmetrie van het verkeersbord. In plaats van het verkeersbord zelf als studieobject te nemen, neem ik de groep van al zijn symmetrieën als studieobject.
Door de samenwerking van je eigen verwondering en de wiskunde valt een ondoorgrondelijk concept als ‘symmetrieën van symmetrieën’ langzaam op zijn plaats
Zo’n groep symmetrieën bekijk ik op haar beurt als één voorwerp. Ik kan dus ook zoeken naar de symmetrieën van die groep symmetrieën, want een symmetrie is een handeling op een voorwerp waardoor de vorm niet verandert. Dat klinkt misschien wat vreemd en zulke symmetrieën van symmetrieën zijn inderdaad moeilijker te visualiseren, maar het toont een van de fascinerende aspecten van wiskundig onderzoek: hoe door de samenwerking van je eigen verwondering en de wiskunde een ondoorgrondelijk concept als ‘symmetrieën van symmetrieën’ langzaam op zijn plaats valt.
Mijn eigen fascinatie werd nog meer geprikkeld door het volgende: een constructie die een groep symmetrieën in stukken opdeelt met behulp van een symmetrie van diezelfde groep symmetrieën. In het voorbeeld van het verkeersbord leveren sommige symmetrieën van de groep symmetrieën drie stukken op; andere leveren vijf stukken op. Andere aantallen zijn onmogelijk voor het geval van het verkeersbord. We vatten die informatie samen in een verzameling getallen, in dit geval {3, 5}, en koppelen die ten slotte aan de groep symmetrieën.
Mijn concrete puzzel
Hoewel die constructie al langer bestaat, zijn er nog veel onbeantwoorde vragen over het verband tussen een groep symmetrieën en haar gekoppelde verzameling getallen. Dat verband gedraagt zich niet zoals je zou verwachten: een cel van een honingraat (een regelmatige zeshoek) en een stopbord (een regelmatige achthoek) hebben bijvoorbeeld allebei meer symmetrieën dan een vierkant, maar hun verzamelingen getallen zijn respectievelijk {4, 6} en {3, 5, 7}. Als een groep symmetrieën groter is dan een andere, is de verzameling getallen dus niet noodzakelijk ook groter.

Voorwerpen met meer symmetrieën leveren niet noodzakelijk grotere verzamelingen getallen op.
In mijn onderzoek achterhaalde ik op welke manieren het verband tussen de groep symmetrieën en haar verzameling getallen zich wel gedraagt zoals we verwachten. Daardoor weten we bijvoorbeeld precies hoe de verzameling getallen eruitziet als we vertrekken van de groep symmetrieën van een regelmatige veelhoek, of dat nu een vierhoek, een zeshoek, of een 1997-hoek is. We weten ook wanneer hij groter is en wanneer niet.
Het nut van nutteloos onderzoek
Is mijn onderzoek nu nuttig? Voor jou, op dit moment, hoogstwaarschijnlijk niet – maar wel voor andere wiskundigen. Voor hen bewijst het trouwens al zijn (bescheiden) nut, want daardoor hebben zij al een paar van hun puzzels kunnen leggen. Zal mijn onderzoek zijn nut ook tonen in het dagelijkse leven? Misschien wel, misschien niet. De verschillende wiskundige puzzels zijn nauw verweven, zowel met elkaar als met puzzels uit andere wetenschappen, zoals de fysica of de ingenieurswetenschappen. Door die verwevenheid kan mijn onderzoek zich na verloop van tijd een weg banen naar toepassingen in onze wereld, net zoals dat in het verleden al meerdere keren gebeurd is met andere zuivere wiskunde.
De wereld overstelpt ons met haar problemen, haar puzzels; wiskundig onderzoek levert soms gewoon een aantal passende puzzelstukjes aan. Weten we voor welke van die puzzels? Nee. Weten we altijd of die puzzel überhaupt bestaat? Nee, maar ook dat houdt wiskundigen niet tegen. De geschiedenis leert ons dat de juiste puzzel altijd kan opduiken, al is het pas na een paar jaar, een paar decennia of een paar eeuwen. Intussen werken de wiskundigen van nu door hun onderzoek verder aan nieuwe stukjes. Het enige wat we hen moeten gunnen, is een beetje tijd. Misschien valt de puzzel dan ooit vanzelf op zijn plaats.
Pieter Senden dingt mee naar de Vlaamse PhD Cup 2023. Ontdek meer over dit onderzoek op www.phdcup.be.



