Over coureurs, brouwers en heksen

- Een gastbijdrage van collega Stijn Dierckx - 

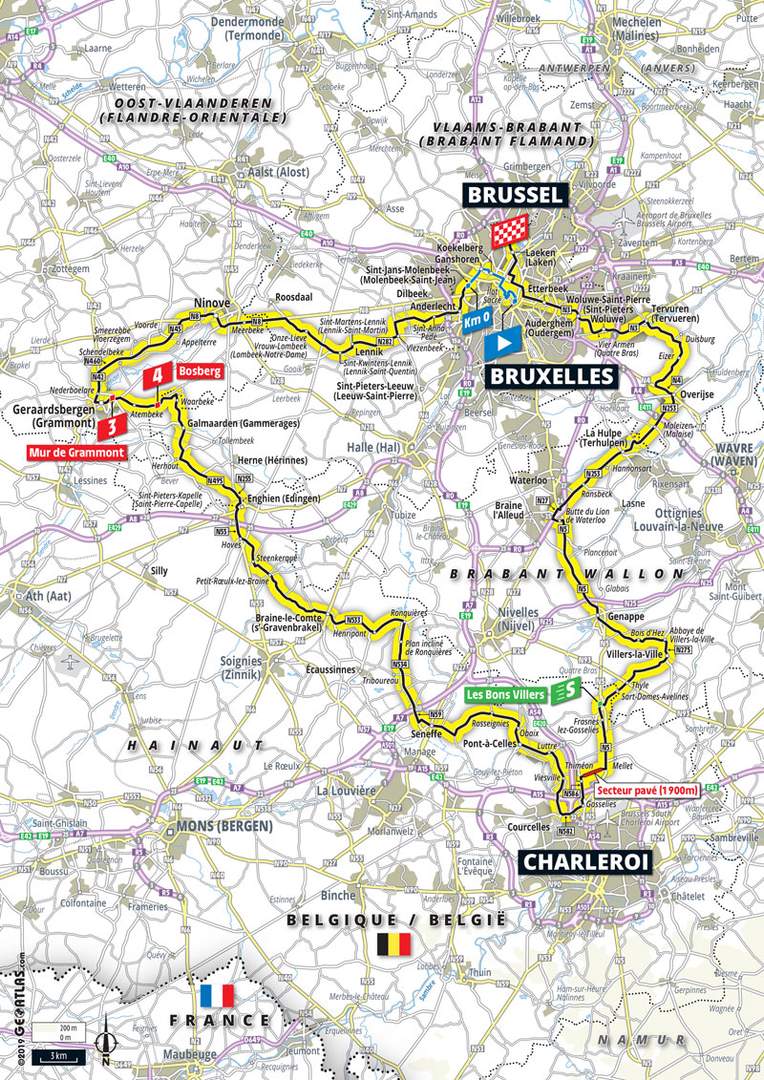
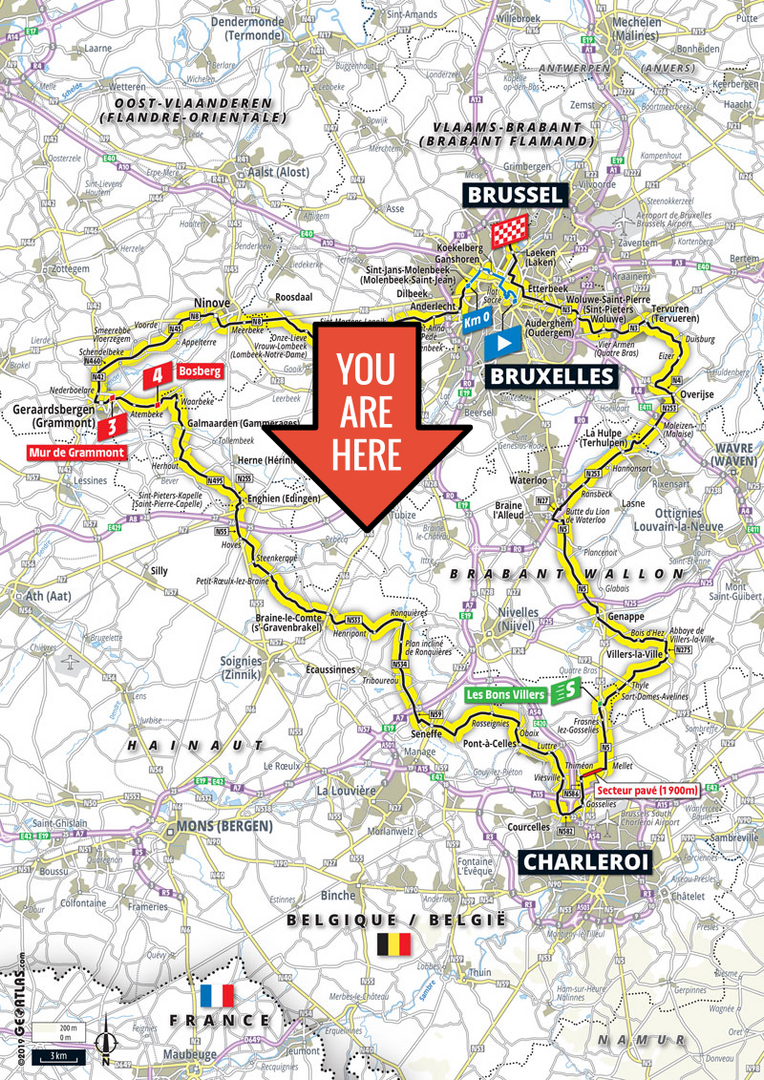
Je kon er zo goed als niet naast kijken begin juli: de 106e Tour de France streek neer in hartje Brussel voor le Grand Départ, 50 jaar na de eerste tourzege van Eddy Merckx. De eerste etappe startte in Brussel om via de Muur van Geraardsbergen langs Charleroi een lus te maken en terug in Brussel aan te komen. Niets vreemds, zo op het eerste gezicht. Maar de opmerkzame kijker van het omkaderingsprogramma Vive le Vélo hoorde het Karl Vannieuwkerke al zeggen in de nabeschouwing van die etappe: "Als je die rit op de kaart gaat bekijken, kom je bijna bij de vorm van ons land uit. Kijk naar die contouren, dit lijkt wel België. Zou dit toeval zijn, of een folietje van de parcoursbouwer?" Het antwoord op die vraag moeten we u schuldig blijven, maar feit is wel dat de gelijkenis enigszins treffend is. Oordeelt u vooral zelf:

De wielrenners zullen er die dag allicht niet al te veel aandacht aan besteed hebben, maar wiskundigen zitten (zoals op zovele vlakken) nu eenmaal anders in elkaar. Bij ons deed dit amusante fait divers wel een (fiets)belletje rinkelen, namelijk dat van de Fixpuntstelling van Brouwer. Deze stelling, die we u iets verder voorschotelen, heeft toepassingen in de wiskunde, de fysica, de logica, maar evengoed in de biologie en de economie.  Inderdaad, de vaste punt-stelling was essentieel in de economie bij het bewijs van het bestaan van marktevenwichten (? Ik ben geen economist). Kenneth Arrow en Gérard Debreu kregen hiervoor de Nobelprijs economie in 1983. Ze werd ook gebruikt in het originele bewijs van het bestaan van Nash-evenwichten, waarvoor John Forbes Nash Jr. (de man van de film A Beautiful Mind) de Nobelprijs economie kreeg. Maar wat zegt die stelling nu precies? In haar meest eenvoudige vorm (?):

Stelling
Een continue functie van een convexe en compacte deelverzameling van een Euclidische ruimte naar zichzelf heeft ten minste één fixpunt, i.e. een punt dat op zichzelf wordt afgebeeld. 

Niet erg verhelderend, tenzij u als lezer bekwaam bent in algebraïsche topologie of aanverwanten. Een eenvoudigere uitleg is met andere woorden meer dan op zijn plaats.
We bekijken het simpelste geval, namelijk een continue functie $f$ van het gesloten interval $[0,1]$ in zichzelf. Dit zijn functies die we eenvoudig kunnen voorstellen met behulp van een grafiek zoals we in de middelbare school maar al te vaak moesten doen. Twee voorbeelden van zo'n continue functies van $[0,1]$ naar zichzelf ziet u hieronder:

In essentie gaat het hier over. Vertrek van een vierkant, en teken een vloeiende (gebogen) lijn (zonder uw pen op te heffen) die van de linkeronderhoek loopt naar de rechterbovenhoek (rood) of van de linkerbovenhoek naar de rechteronderhoek (blauw) zonder terug te keren: u tekent dus van links naar rechts.

De Fixpuntstelling van Brouwer zegt nu dat deze functies een fixpunt hebben, met andere woorden dat hoe u die lijn ook tekent, er zal zeker minstens 1 punt op liggen waarvoor de afstand tot de linkerzijde van het vierkant gelijk is aan de afstand tot de onderste zijde. De punten in het vierkant die hieraan voldoen, zijn in het groen aangeduid. De stelling zegt dus met andere woorden dat de blauwe en de rode functies de groene lijn ergens moeten snijden, wat duidelijk te verifiëren is op de tekening. 

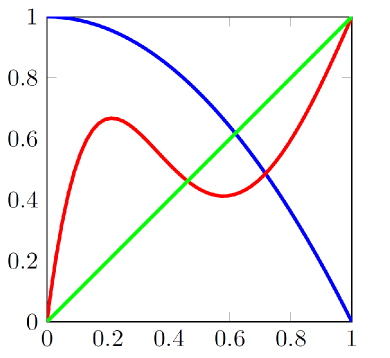
De stelling zegt niets over waar dit fixpunt zich bevindt in het interval, noch over hoeveel van die fixpunten er zijn. De blauwe functie heeft er inderdaad exact eentje, maar als u goed kijkt, kan u zien dat de rode functie er zelfs drie heeft!

Waarom de naam fixpunt? Wel, dat kunnen we laten zien door de informatie op de figuur anders te interpreteren. Met elk punt op de horizontale as wordt een hoogte geassocieerd (af te lezen op de verticale as). En als we nu (bijvoorbeeld in het geval van de blauwe functie) die twee assen anders tekenen, dan kan je op de volgende figuur via de pijlen zien hoe die associatie precies gebeurt. (Links de horizontale as, rechts de verticale.)

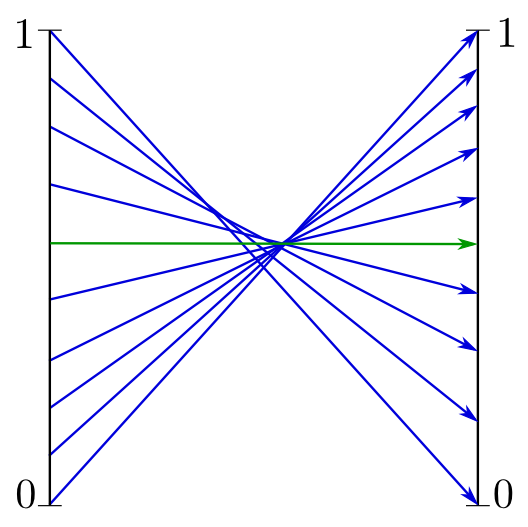
En je ziet dat er een punt is links dat op dezelfde hoogte terechtkomt rechts: de groene pijl. De hoogte blijft dezelfde: een vast punt of fixpunt! Als de functie continu is, en de grafiek ononderbroken, dan is er steeds zo'n vast punt. Dat is wat de stelling van Brouwer zegt.

Nog niet concreet genoeg? We doen nog een poging. Het is vakantie, en je hebt zin om een berg te beklimmen. Je vertrekt onderaan de berg (met je tentje) om 10u, en stapt via het pad naar boven. Om 18u heb je de top bereikt, je geniet wat van het uitzicht, eet en drinkt iets, om dan in je tent de nacht door te brengen. De volgende ochtend sta je klaar om de berg af te dalen. Je vertrekt stipt om 10u en loopt naar beneden. Om 18u sta je opnieuw onderaan de berg, op de plaats waar je de vorige dag vertrokken bent. Wist je dat je er nu zeker van kan zijn dat er ergens een tijdstip is tussen 10u en 18u waarop je zowel bij de beklimming (op de eerste dag dan) als bij de afdaling (op de tweede dag) op dezelfde hoogte was? Inderdaad, en je kan dat ook eenvoudig inzien gebruik makend van een voorbeeld. Neem de figuur met de blauwe en de rode functie. Neem de horizontale as als tijdsas (met als eenheid 10u), en de verticale as als hoogte-as (met eenheid km), en stel dat de berg 1 km hoog is. Je kan dan de rode kromme zien als een voorstelling van de beklimming van de berg (waarbij je even een eindje terug bent moeten gaan wegens onderweg iets verloren). De blauwe kromme is voor de volgende dag, de afdaling. En we hebben beide dagen over elkaar geschoven. Het is duidelijk dat de beide lijnen elkaar moeten snijden, hoe je die ook tekent. Dat snijpunt geeft het moment aan dat je bij beklimming en de afdaling op dezelfde hoogte was. Een gevolg van de stelling van Brouwer.

Ook in meerdere dimensies blijft dit resultaat gelden. In twee dimensies kan men bijvoorbeeld denken aan een ronde schijf (een volle schijf, geen cd) die je een kwartslag draait. Inderdaad, alle punten zijn veranderd van plaats, behalve het middelpunt wat dus ons bewuste fixpunt is!

Hoewel de algemene formulering van deze stelling een van de belangrijkste resultaten is in een zeer abstract deel van de wiskunde, heeft deze toch enkele leuke toepassingen in de realiteit. Dacht u dat het mogelijk was om een kopje koffie met een vleugje melk perfect te mengen door te roeren met een lepeltje? Fout! Na het roeren, wanneer de koffie terug tot stilstand is gekomen, zal er altijd minstens één deeltje in de vloeistof op dezelfde plaats eindigen als waar het vertrokken was voor u begon te roeren. Een gevolg van de Fixpuntstelling van Brouwer (er van uit gaande dat het roeren een continue beweging is, dat het kopje een normale (convexe) en geen exotische vorm heeft, en dat de koffie niet zodanig heet is dat er in tussentijd vloeistof is kunnen verdampen)!

Een andere toepassing is het volgende: neem een landkaart van het land waarin u zich bevindt. Leg deze kaart gewoon vlak op tafel. Er zal dan, opnieuw dankzij de Brouwer Fixpuntstelling, een Je bent hier!-punt bestaan op deze kaart dat exact overeen komt met de plaats waar u zich in het echt bevindt. De logica zelve natuurlijk. We doen het op kleinere schaal. Haal even een plan van het dorp/de stad waar u woont boven, leg dat plan op de tafel in de keuken en zoek op dat plan naar de straat waar u woont, meer bepaald naar de plaats waar uw huis staat, meer bepaald naar de plaats waar de keuken ligt (veronderstel dat je willekeurig goed kan inzoomen op dat plan), meer bepaald naar de plaats waar de tafel in je keuken staat. Teken daar een punt. Onder dat punt staat (a) je tafel op het plan (b) je tafel in je huis. Een vast punt dus! (Voor wiskundepuriteinen - je moet nog even verder inzoomen om het goed te doen). Terugkerend naar die eerste etappe van de Ronde van Frankrijk: er is dus (minstens) een punt binnen (niet per se op) het parcours van deze etappe, er van uit gaande dat dit een verkleining is van de contouren van België, dat op zichzelf afgebeeld is.

Een laatste opmerkelijk feit is dat de Fixpuntstelling van Brouwer ook verbanden heeft met totaal andere wiskundige domeinen, bijvoorbeeld speltheorie. Het is namelijk zo dat deze stelling equivalent is met het feit dat het bordspel Hex niet kan eindigen in een gelijkspel. 

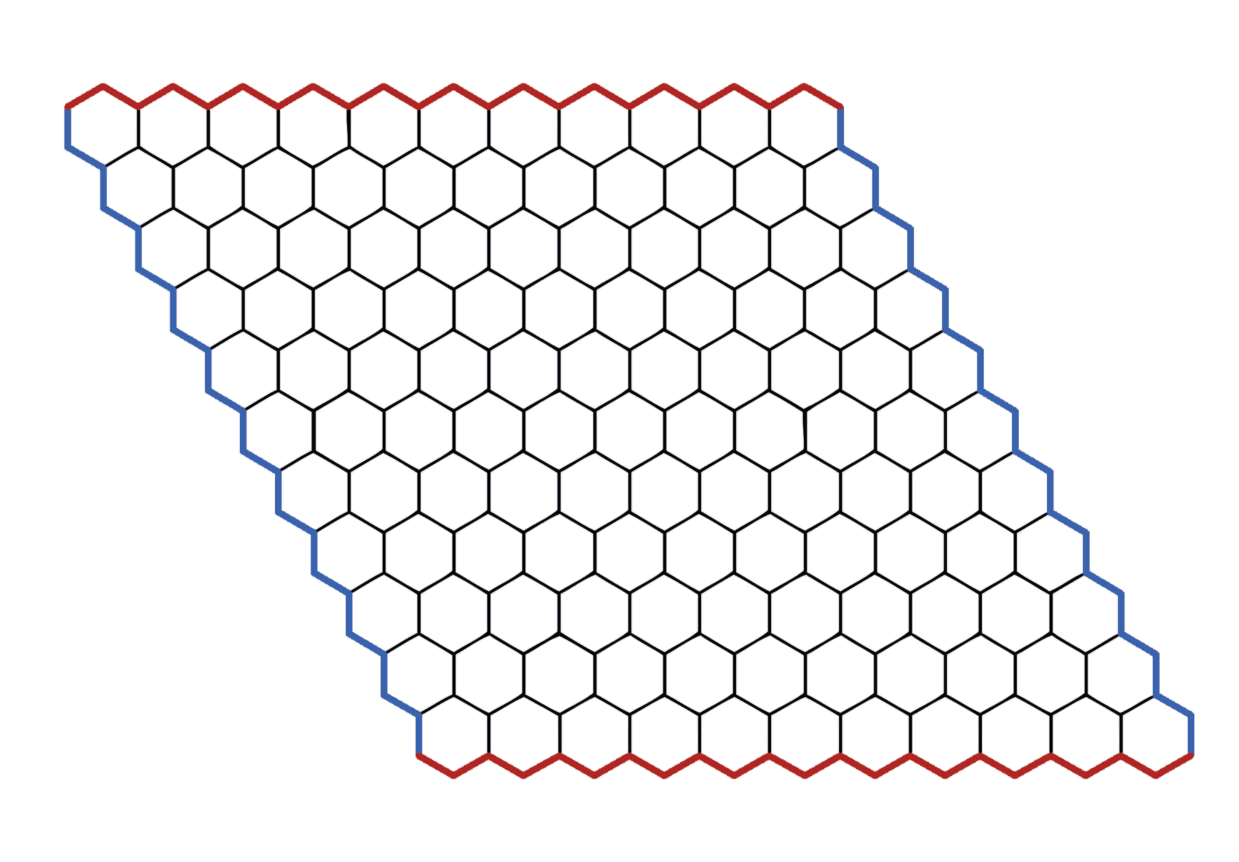
Het spel Hex werd uitgevonden in de jaren veertig, onafhankelijk door de bekende speltheoreticus John Nash (diezelfde van daarstraks), en door Piet Hein (Piet Hein, zijn naam is klein, al gaat het hier niet over de Nederlandse admiraal van de Zilvervloot, maar wel over zijn naamgenoot en afstammeling, de Deense wiskundige).
Om het spel te spelen, heb je naast een tegenstander ook een bord nodig bestaande uit 11 bij 11 zeshoekige tegels zoals op de afbeelding hierboven. De twee spelers plaatsen om beurt een steen van hun kleur (in dit geval rood of blauw) op het bord, en proberen om het eerst de zijden van hun kleur met elkaar te verbinden door middel van een onafgebroken ketting stenen van dezelfde kleur. In het spel hieronder is de blauwe speler de winnaar.

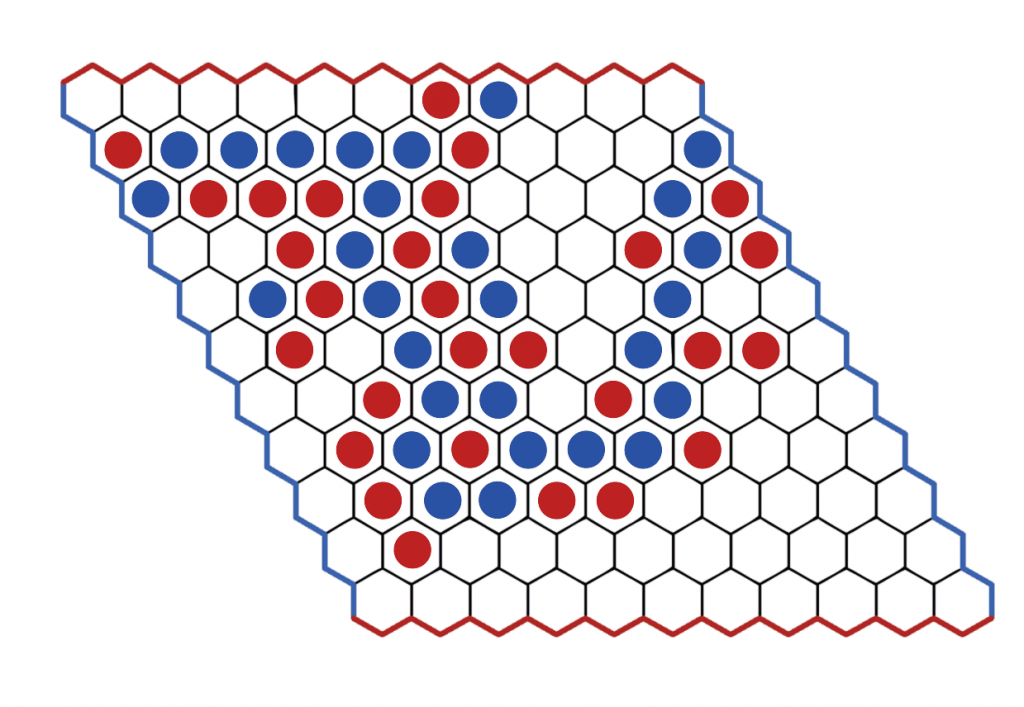
Het spel Hex blijft tot op vandaag onderwerp van wiskundig onderzoek in verschillende domeinen. Zo zijn er tot op vandaag winnende strategieën ontwikkeld voor alle openingszetten op een $7\times7$-bord, $8\times8$-bord en $9\times9$-bord. Hoewel het spel zeer eenvoudig uit te leggen valt, is de complexiteit dus enorm. Er zijn ongeveer $2.4\times 10^{56}$ mogelijke legale posities, wat een stuk meer is dan de $4.6\times 10^{46}$ mogelijkheden bij schaken. Er zit dan ook heel wat strategie achter om een spel als winnaar te beëindigen, en men moet zeer complexe patronen kunnen analyseren om potentiële verbindingen te kunnen creëren.

De equivalentie tussen de beslisbaarheid van het Hex-spel en de Fixpuntstelling van Brouwer is niet gemakkelijk om aan te tonen (Zie hiervoor David Gale (1979). "The Game of Hex and Brouwer Fixed-Point Theorem." The American Mathematical Monthly. Mathematical Association of America. 86 (10) p. 818-827). Wel kunnen we op een relatief eenvoudige wijze laten zien dat een spelletje Hex inderdaad altijd een winnaar heeft op het einde. Maar misschien wil u het zelf eerst even proberen?
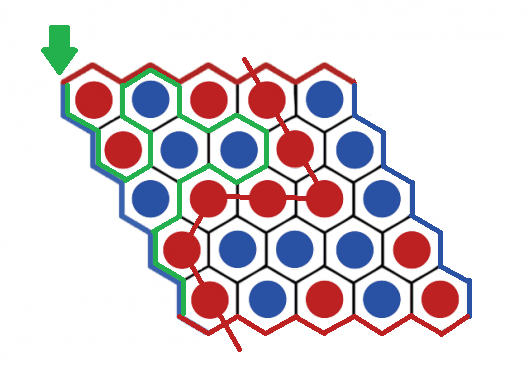
Indien niet, dan volgt nu een spoiler. We beginnen we met een volledig gevuld spelbord waarin elke tegel een rode of blauwe steen bevat. We gaan dan een pad tekenen (in het groen) tussen de tegels met verschillende kleuren, te beginnen linksboven in de hoek.

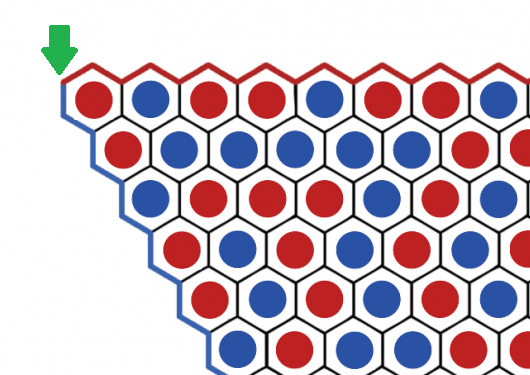
Beschouw de randen van het bord als muren van stenen uit de respectievelijke kleur. In ons voorbeeld gaat het pad de eerste vier stappen dus telkens naar onder, tussen de rode stenen en de blauwe muur:

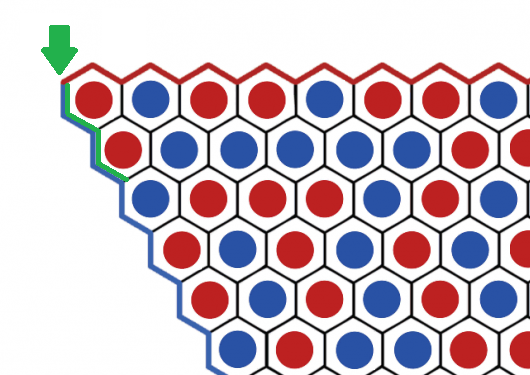
Nadien veranderen we van richting, aangezien we telkens willen grenzen aan een rode én een blauwe steen tegelijk. De rest van het groene pad op dit stukje van het speelbord is hieronder uitgetekend.

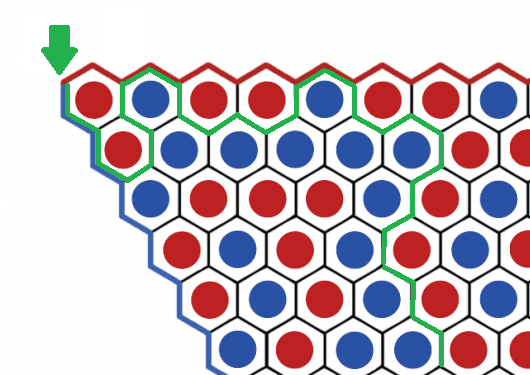
We kunnen nu enkele zaken opmerken:

• Het groene pad zal zichzelf nooit snijden of een lus vormen. Als dat wel zo zou zijn, zou minstens een stukje van het pad langs twee stenen van dezelfde kleur gaan, wat door de regels van de constructie van het groene pad niet kan. Het pad moet dus ergens eindigen.

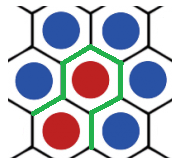
Stel bijvoorbeeld dat we in het voorbeeldje hier weergegeven aangekomen waren onderaan tussen de rode en de blauwe steen. Aangezien de andere stenen rond de middelste rode steen allemaal blauw zijn, kunnen we bijna helemaal rond gaan met ons groene pad. Maar, het laatste stukje van de lus kan onmogelijk vervolledigd worden, aangezien we terug aankomen bij de onderste rode steen en niet tussen de twee rode stenen mogen gaan met de groene lijn.

• Het pad kan nooit in het midden van het bord eindigen. Inderdaad, een kruispunt waar het groene pad aankomt, grenst aan drie tegels, waarvan er (per constructie) twee een andere kleur steen bevatten. De derde steen verschilt dus van kleur met een van deze twee stenen, waardoor het pad telkens kan worden voortgezet.

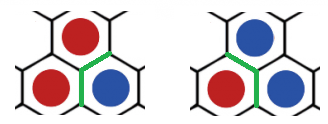
• Analoog kan ingezien worden dat het pad ook niet kan eindigen aan een van de randen van het bord, aangezien dat deze verondersteld worden om een solide muur van één enkele kleur te vormen. Je kan dus altijd verder gaan naar de kant van de steen die van kleur verschilt met de muur waar je tegen botst.

De enige mogelijkheid die dus nog rest, is dat het pad eindigt in een van de andere hoekpunten van het spelbord.

Merk ook op dat de stenen vlak naast het pad aan een kant telkens rood zijn en aan de andere kant telkens blauw. In het voorbeeld hierboven is de linkerkant rood en de rechterkant blauw, als we kijken vanuit het standpunt van de eenzame fietser die kromgebogen over zijn stuur tegen de wind zichzelf een groene weg baant, vertrekkend aan de groene pijl. Hierdoor kan het groene pad nooit eindigen in de hoek rechtsonder, aangezien we daar zouden moeten aankomen met rood langs rechts en blauw langs links. 

Er blijven dus nog twee mogelijke eindpunten over, zijnde de twee overblijvende hoekpunten van het speelbord. Stel nu dat het pad eindigt in het hoekpunt linksonder. Dat wil zeggen dat de blauwe muur links volledig afgescheiden is van de rest van het speelbord door een onafgebroken keten van rode tegels aan de andere kant van het groene pad. Met andere woorden, de rode speler heeft gewonnen. Zie hieronder voor een fictief voorbeeldje op een $5\times5$-bord.

In het geval dat het pad rechtsboven eindigt, zijn de rollen natuurlijk omgedraaid en heeft blauw gewonnen. In ieder geval, het volledig gevulde speelbord bevat hoe dan ook een winnaar.