$\pi$-dag, 14 maart, is tegelijk de internationale dag van de wiskunde. En op die dag mogen er dus wat wiskundige formules te zien zijn, zeker als ze iets te maken hebben met het getal $\pi$.
Wist je al dat ...
$\ldots$ je vandaag taart (`pie') moet eten, of nog beter: trakteren met taart op je werk?
$\ldots$ het getal $\pi$ de verhouding geeft van de omtrek van een cirkel tot de diameter, maar ook de verhouding van de oppervlakte van die cirkel tot het kwadraat van zijn straal?
$\ldots$ het getal $\pi$ tot op 500 cijfers na de komma gelijk is aan:

$\ldots$ de volgende uidrukking uit een boek van 1593 een formule is voor het getal $\pi$?

$\ldots$ de beroemdste formule voor het getal $\pi$, de bovenste van de twee onderstaande formules, de formule van Madhava-Gregory-Leibniz, varianten heeft waarbij in het rechterlid gewoon wat termen van teken zijn veranderd?
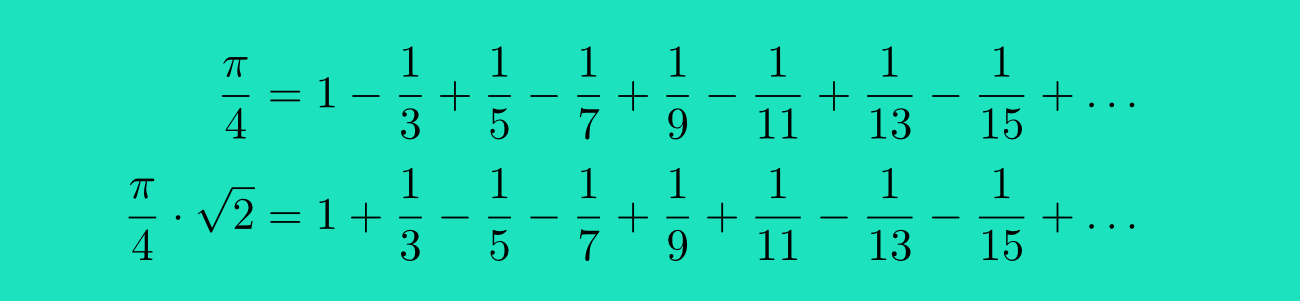
$\ldots$ de bekende benadering voor $\pi$ die maar 2 verschillende cijfers gebruikt, nl. $\frac{22}{7}$, op spectaculaire wijze moet onderdoen voor de volgende formule van de Indische wiskundige Srinivasa Ramanujan?
$$\frac{22}{7} = 3.1428571\ldots \ \ \mbox{maar} \ \ \ \frac{9}{5} + \sqrt{\frac{9}{5}}= 3.1416407\ldots$$
$\ldots$ de wiskundige Benjamin Peirce (1809-1880) zich in 1864 verbaasde over de formule links die laat zien dat een complexe macht van een complex getal een reëel resultaat kan geven?
$$
{\rm i}^{-\rm i} = \sqrt{\text{e}^{\pi}} \hspace{1.5cm} \hspace{1.5cm} \text{e}^{-{\rm i} \pi}= -1
$$
Hierbij is $\rm i$ de complexe eenheid (met dus ${\rm i}^2 = -1$).
Peirce zei erover tegen zijn studenten: Gentlemen, we have not the slightest idea what this equation means, but we may be sure that it means something very important. Diezelfde Amerikaanse wiskundige zei naar verluidt over de formule rechts: Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don't know what it means. But we have proved it, and therefore we know it must be the truth.
$\ldots$ het record berekende decimalen van het getal $\pi$ in 2024 alweer gesneuveld is? Twee verbeteringen sinds $\pi$-dag 2024: 105 000 000 000 000 decimalen op 14 maart ($\pi$-dag), en 202 112 290 000 000 decimalen op 28 juni ($\tau$-dag;-). Twee keer door hetzelfde bedrijf voor gegevensopslag. Ze gebruikten de bovenste formule:
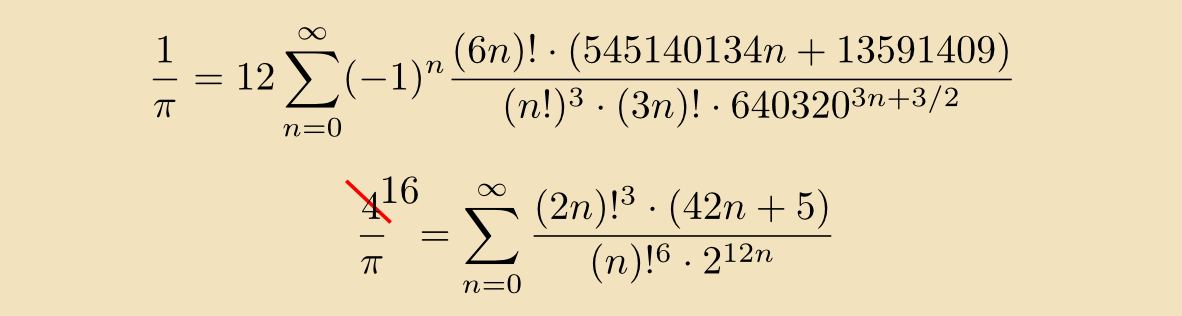
Elke extra term van deze oneindige som geeft 14 extra decimalen. Deze som is gerelateerd aan de onderste formule, alweer van de hand van Srinivasa Ramanujan. Deze laatste formule heeft de status van BF (Bekende Formule) sinds ze in de Disney-film High School Musical, die zich afspeelt in een school, te zien is op een schoolbord, en een van de leerlingen aan de lerares vraagt: ``Moet in die tweede vergelijking niet staan: 16 gedeeld door $\pi$?". Waarop de lerares haar rekentoestel bovenhaalt, begint te rekenen, en de fout verbetert.
$\ldots$ $\text{e} \ (=2.718281828\ldots)$ knopen een goede benadering is voor $\pi$ mijlen per uur? (zie xkcd)
$\ldots$ twee Indische fysici, Arnab Priya Saha en Aninda Sinha van het Indian Institute of Science, die onderzoek doen in snaartheorie, in 2024 per toeval een nieuwe formule hebben ontdekt voor het getal $\pi$:
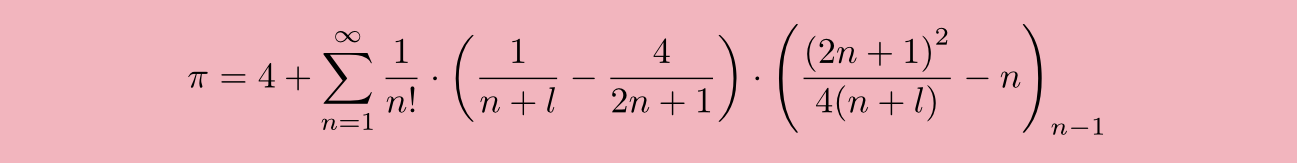
Hierbij moet je de uitdrukking $(a)_{n-1}$ interpreteren als het product $a (a+1) (a+2)\ldots (a+n-2)$. De $l$ die voorkomt in de formule is een (positieve) parameter, waarvan je de waarde vrij mag kiezen. Deze formule is origineel in de zin dat er geen andere formules voor $\pi$ bekend zijn die een vorm hebben die op deze lijkt.
$\ldots$ stand-up mathematician Matt Parker in 2024 geprobeerd heeft om het record decimalen-van-$\pi$-met-de-hand-berekenen te breken. Dat record stond (staat) op naam van William Shanks die in 1873 aan 707 decimalen zat. Pas in 1946 bleek dat er maar 527 juist waren, en die had hij al gevonden in 1853. Shanks gebruikte de formule van John Machin:
$$
\frac{\pi}{4} = 4 \cdot {\rm Bgtg} \frac{1}{5} - {\rm Bgtg} \frac{1}{239}
$$
in combinatie met de volgende oneindige som voor ${\rm Bgtg} \frac{1}{m}$:
$$
{\rm Bgtg}\frac{1}{m} = \frac{1}{m}-\frac{(\frac{1}{m})^3}{3}+\frac{(\frac{1}{m})^5}{5} - \frac{(\frac{1}{m})^7}{7} +\frac{(\frac{1}{m})^9}{9} - \ldots
$$
(Bgtg is de toets tan$^{-1}$ op je rekenmachine). Matt Parker dacht het beter te kunnen door met een hele ploeg rekenaars (400) te werken, en met een formule die sneller convergeerde:
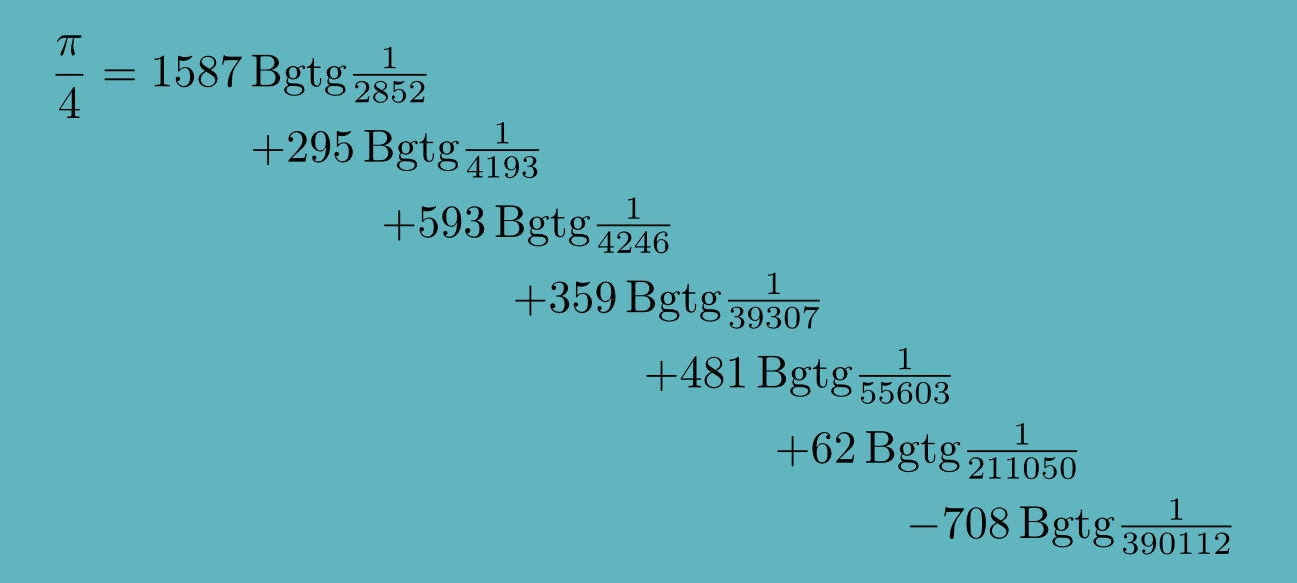
om zo het rekenwerk te kunnen parallelliseren. Het record werd niet gebroken, 139 decimalen werden berekend.
$\ldots$ AI en $\pi$ blijkbaar goed samengaan? Je kan The Ramanujan Machine bekijken als een AI-wiskundige. Sinds 2021 genereert dit computerprogramma kettingbreuken (= oneindig voortlopende breuken) voor de bekendste wiskundeconstanten, waaronder natuurlijk $\pi$. Het bewijs dat de gegenereerde formules correct zijn, dat wordt overgelaten aan de echte wiskundigen. Dit is zo'n formule:
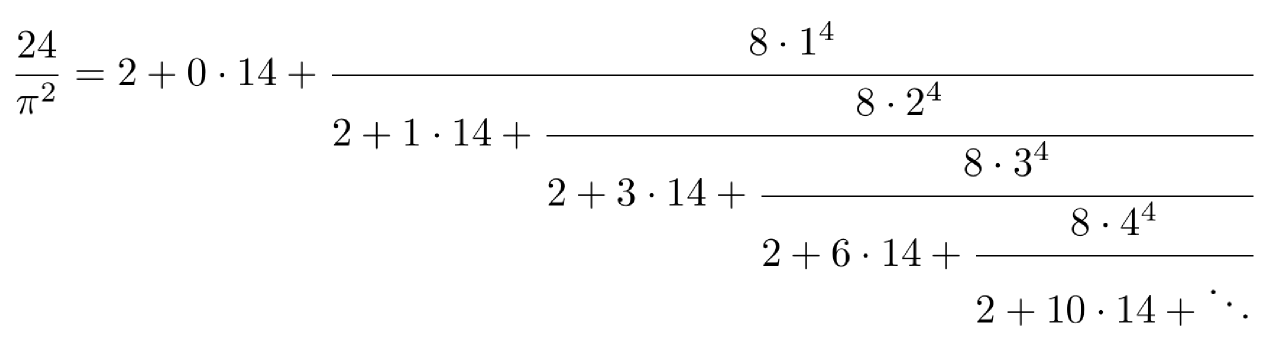
waarbij de factoren van 14, nl. 0, 1, 3, 6, 10 de driehoeksgetallen zijn: het $n$-de getal is $n$ meer dan het vorige, en we starten vanaf het nulde getal 0.
$\ldots$ er een schat aan informatie over $\pi$ te vinden is in de OEIS (Online Encyclopedia of Integer Sequences)? Bijvoorbeeld een rij getallen die zo begint:
$$
{\small 1, 16470, 44899, 79873884, 711939213, 36541622473, 45677255610, 62644957128, 656430109694, \ldots}
$$
Nemen we een willekeurige term van deze rij, bijvoorbeeld $44899$, dan mag je zeker zijn dat de 5 decimalen van $\pi$ vanaf de $44899^{\rm{e}}$ gegeven zijn door $44899$.
$\ldots$ je de betekenis van de bannerafbeelding van deze blogpost kan terugvinden in onze andere blogpost van vandaag: "Het bijzondere van normale getallen"?
$\ldots$ dat het woord pikant wel degelijk iets te maken heeft met $\pi$?

Met dank aan Cris, Stijn, Nien en Jan voor hun bijdragen $\ldots$



