De kloof tussen taal en wiskunde gedicht

Poëzie is van alle tijden, culturen en talen. Poëzie is van de mensen, voor de mensen. En ook al lijkt het vaak alsof wiskundigen niets met taal hebben, of taalkundigen niets met wiskunde: niets is minder waar. Net zoals wij als wiskundige van tijd tot tijd al wel eens graag van een goed gedicht genieten, zijn er voldoende voorbeelden te vinden van poëten die niet onder stoelen of banken steken dat zij ook een boon hebben voor wiskunde (of andere exacte wetenschappen). We delen met plezier een overzichtje van enkele van onze favoriete schrijfsels.

Poëzie ontstond reeds lang voor er sprake was van het schrift. Verhalen werden vroeger meestal mondeling doorverteld, en door specifieke versvormen of rijm te gebruiken werd het makkelijker om die verhalen juist te onthouden. Maar wat kan dienen voor verhalen, kan natuurlijk ook dienen voor ingewikkelde formules! Zo ontdekte Niccolò Tartaglia zo’n 500 jaar geleden een formule om bepaalde derdegraadsvergelijkingen op te lossen. Zijn collega wiskundige Girolamo Cardano wou deze formule ook wel kennen, en beloofde om de formule niet te publiceren. Tartaglia ging overstag, en deelde de formule in een brief, zij het in gedicht-vorm:

Wat Tartaglia hier in feite op ietwat cryptische wijze omschrijft, is dat je de oplossing van een vergelijking $x^3+px+q=0$ (met $p$ en $q$ willekeurige getallen) kan vinden door middel van een ingenieus trucje. Uiteindelijk leidt dit tot de eerder ingewikkelde oplossing $x = \sqrt[3]{\frac{-q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} + \sqrt[3]{\frac{-q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$, wat Cardano ook wist te ontcijferen. Hij publiceerde de formule toch onder zijn eigen naam, waardoor een grote ruzie ontstond tussen beide heren. (Meer daarover kan je in deze eerdere blogpost lezen.) Een (Engelse) vertaling van het gedicht, inclusief de volledige wiskundige betekenis, kan je in dit artikel vinden.

In diezelfde categorie van geheugensteuntjes spraken we twee jaar geleden op pi-dag ook reeds over enkele gedichten die werden ontwikkeld om de decimalen van het getal pi te onthouden. Maar wie onze pi-weetjes aandachtig heeft gevolgd de laatste jaren (2019, 2018), weet dat er ook heel wat andere pi-gedichten (of piëzie?) bestaan, zoals bijvoorbeeld het gedicht “Pi” van Nobelprijswinnares Wisława Szymborska. Een van de mooiste voorbeelden is echter het gedicht “Decimalen” van de Zwitserse (doch Nederlandstalige) taalvirtuoos en cabaretier Heinz Polzer, beter bekend als Drs. P., later door hem ook op muziek gezet als “Griekse tango”:

“Decimalen” verscheen onder andere in de dichtbundel “Wis- en natuurlyriek” van Drs. P. en Marjolein Kool. Beide auteurs weten daarin op magistrale wijze en met een gezonde dosis humor verschillende onderwerpen en personen uit de wiskunde, natuurkunde en scheikunde in poëzie te verwerken, en waar nodig laagdrempelig toe te lichten met de nodige kennis van zaken. Via deze link kan je een beperkt voorbeeld van de bundel bekijken. Van Marjolein Kool delen we graag het gedicht “Bewijzen” (ter info: een bewijs uit het ongerijmde is een bewijsmethode uit de wiskundige logica, waarbij men er van uit gaat dat een bepaalde stelling niet waar is, door die aanname op een contradictie stoot, en dus besluit dat de stelling in kwestie wel waar moet zijn):

Een bolleboos riep laatst met zwier
gewapend met een vel A-vijf:
‘Er is geen allergrootst getal,
dat is wat ik bewijzen ga.
Stel, dat ik u nu zou bedriegen
en hier een potje stond te jokken,
dan zou ik zonder overdrijven
het grootste kunnen op gaan noemen.
Maar ben ik klaar, roept u gemeen:
“Vermeerder dat getal met twee!”
Dan zien we zeker en gewis
dat dit toch niet het grootste was.
En gaan we zo nog door een poos,
dan merkt u: dit is onbegrensd.
En daarmee heb ik q.e.d.
Ik ben hier zo gelukkig door.
Zo gaan,’ zei hij voor hij bezwijmde,
‘bewijzen uit het ongedichte.’

Het hoeft niet te verbazen dat er nog meer wiskundige stellingen in poëzie werden gegoten. Een van de creatievelingen die beide domeinen ten volle beheerste, was Sir Frederick Soddy (tevens ook winnaar van de Nobelprijs voor Chemie in 1921). Hij herontdekte in 1936 een stelling die reeds door René Descartes in de 17^e eeuw gekend was. Stel namelijk dat je drie cirkels hebt die elkaar raken (de zwarte cirkels in de figuur hieronder), dan zijn er twee mogelijkheden om nog een vierde cirkel (in het rood) te tekenen die ook raakt aan de drie zwarte: een kleine binnenin en een grote eromheen.

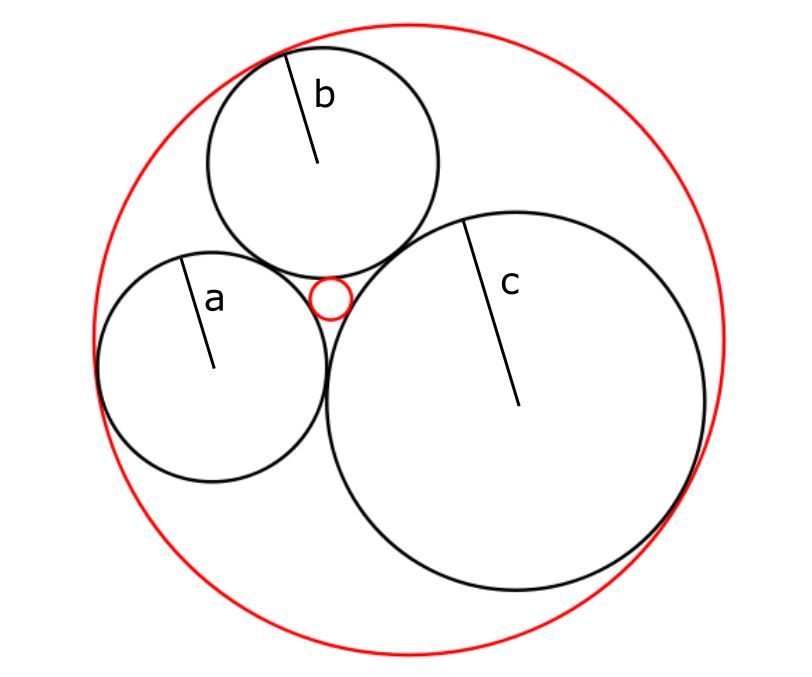
Zij nu $a$, $b$ en $c$ de straal van de zwarte cirkels, dan geldt voor de straal $r$ van een van de rode cirkels steeds dat $\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{1}{r^2} = \frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{r}\right)^2$. Soddy werd met deze stelling vooral beroemd door de wijze waarop hij ze aan de buitenwereld bekend maakte: door middel van het gedicht “The Kiss Precise”. Later werd deze stelling zelfs nog veralgemeend, waarbij het gedicht telkens op gepaste wijze werd uitgebreid: eerst door Thorold Gosset (1937) die een gelijkaardig verband beschreef in een willekeurig aantal dimensies, en nadien door Fred Lunnon (2001) die ook elliptische en hyperbolische meetkunde mee in beschouwing nam.

Een ander voorbeeld is de beroemde laatste stelling van Fermat, die stelt dat een vergelijking van de vorm $x^n+y^n=z^n$ nooit een oplossing heeft waarbij $x$, $y$ en $z$ positieve gehele getallen zijn indien $n$ groter is dan 2. Zelf had Fermat deze stelling in de marge van een boek geschreven, met de gevleugelde woorden “Ik heb een werkelijk opmerkelijk bewijs voor deze stelling, maar deze marge is te klein om het neer te schrijven.”, wat in feite ook als poëzie in de oren klinkt. Echter, het duurde meer dan 350 jaar eer de stelling formeel werd bewezen door Andrew Wiles (in twee artikels die samengeteld maar liefst 129 pagina’s tellen...) door gebruik te maken van elliptische curves, modulaire vormen en andere ingewikkelde wiskundige technieken. Ter ere van deze heuglijke gebeurtenis, een van de belangrijkste wiskundige prestaties van de 20^e eeuw, werd een poëzie-uitdaging uitgeschreven, waar onderstaande limericks uit voortvloeiden:

With an integer greater than 2
It's something one simply can't do.
If this margin were fat,
I'd show you all that,
But it's not, so the proof is on you!
(Ted Munger)

We take an elliptic curve E,
Consider the points killed by 3,
This "rho" must be modular,
And by facts which are popular,
The proof of Fermat comes for free.
(Jeremy Teitelbaum)

Dat de limerick-dichtvorm zich uitstekend leent tot wiskunde, wordt ook duidelijk uit onderstaande voorbeelden die regelmatig de ronde doen op sociale media, al is een minimum aan rekenvaardigheid wel nodig om hun genialiteit te verifiëren.

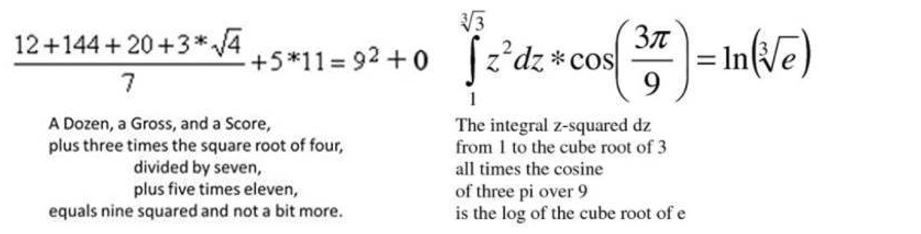
Het moge duidelijk zijn dat de liefde voor de wiskunde een perfecte inspiratiebron is voor heel wat poëzie. De meeste poëzie gaat natuurlijk over de liefde, maar ook dat kan perfect op wiskundige wijze worden uitgedrukt. Zo is er de liefdesverklaring “Finite Simple Group (of Order Two)” van The Klein Four, vol met wiskundige woordspelingen (al heeft dit wel een betrekkelijk groot nerd-gehalte, maar dat geven we zonder schroom toe).  Maud Vanhauwaert (in 2018 en 2019 nog stadsdichteres van Antwerpen) schreef het gedicht “Wij zijn evenwijdig” uit haar gelijknamige bundel, met de prachtige vers “ze haakt haar arm in de mijne tot een lemniscaat”. De lemniscaat van Bernoulli is een kromme die we het best kennen als het symbool voor oneindig $\infty$, wat meteen de symboliek in het gedicht verklaart. Of er is het visuele gedicht “Sacrifice and Bliss” van Kaz Maslanka:

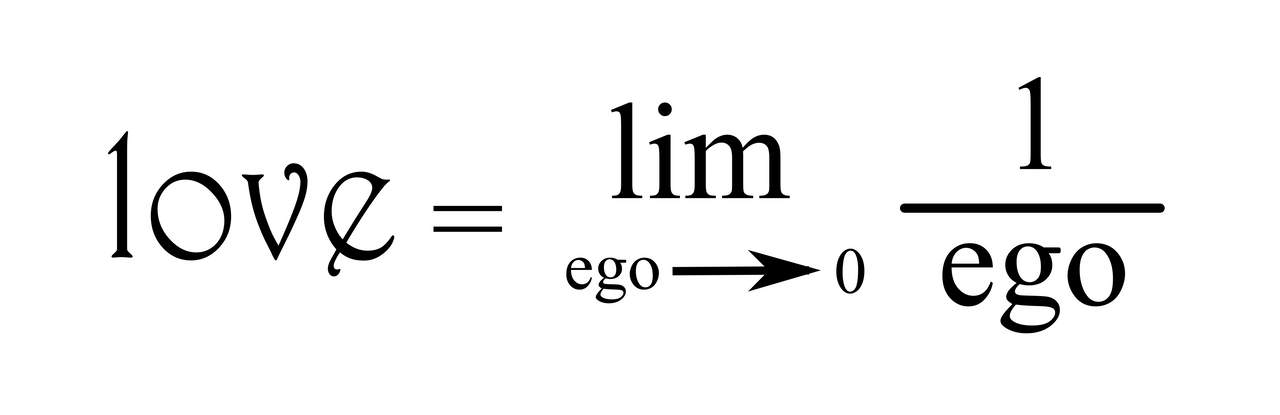
Met een minimum aan woorden slaagt Maslanka er in om de essentie van liefde samen te vatten in een eenvoudige wiskundige formule: als de noemer van de breuk (zijnde het ego) kleiner en kleiner wordt en 0 benadert, zal de breuk zelf groter en groter worden en in de limiet zelfs oneindig groot worden. Anders gezegd: de kracht van de liefde is omgekeerd evenredig met de grootte van het ego.

Nog meer lezen? Hieronder vind je nog andere artikels/blogs/boeken over de combinatie van wiskunde en poëzie:

Nederlandstalig:

• Wis- en natuurlyriek – met chemisch supplement en verse verzen van K. (Drs. P & Marjolein Kool)
• Gedichten uit het ongerijmde (Jeanine Daems)

Engelstalig:

• Poetry Inspired by Mathematics (Sarah Glaz)
• Mathematical Pattern Poetry (Sarah Glaz)
• Mathematics in Poetry (JoAnne Growney)
• Mathematical Poetry (Kaz Maslanka)
• Strange Attractors, Poems of Love and Mathematics (ed. Sarah Glaz & JoAnne Growney)

Franstalig:

• Les mathématiques sont la poésie des sciences (Cédric Villani)